Underdamped Systems
Underdamped systems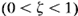 
:
In this case, C(s)/R(s) can be written
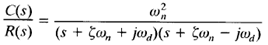
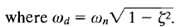The frequency ωd is called the damped natural frequency. For a unit-step input, C(s) can be written
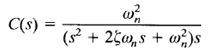
The inverse Laplace transform of the above equation can be obtained easily if C(s) is written in the following form:
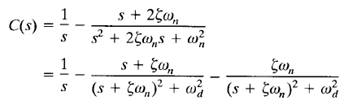
We know that,
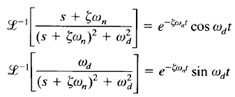
Hence the inverse Laplace transform of the equation of C(s) is obtained as
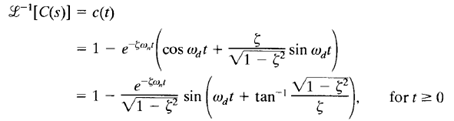
This result can be obtained directly by using a table of Laplace transforms. From Equation above, it can be seen that the frequency of transient oscillation is the damped natural frequency ωd and thus varies with the damping ratio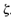 
. The error signal for this system is the difference between the input and output and is
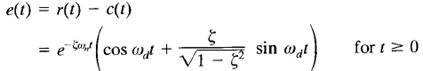
This error signal exhibits a damped sinusoidal oscillation. At steady state, or at t = ∞, no error exists between the input and output.
If the damping ratio 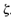is equal to zero, the response becomes undamped and oscillations continue indefinitely. The response c(t) for the zero damping case may be obtained by substituting 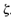= 0 in the inverse Laplace transform of the equation of C(s), yielding
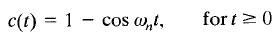
Thus, from the above equation, we see that ωn represents the undamped natural frequency of the system. That is, W n is that frequency at which the system would oscillate if the damping were decreased to zero. If the linear system has any amount of damping, the undamped natural frequency cannot be observed experimentally. The frequency that may be observed is the damped natural frequency ωd, which is equal to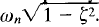 
. This frequency is always lower than the undamped natural frequency. An increase in 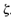would reduce the damped natural frequency ωd. If 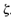is increased beyond unity, the response becomes overdamped and will not oscillate.