Unit-impulse Response Of First-order Systems

Unit-impulse response of first-order systems

 

 

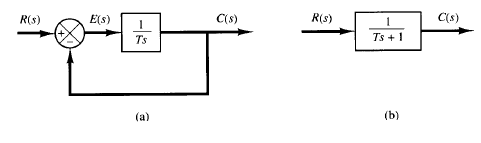
Fig: 1

For the unit-impulse input, R(s) = 1 and the output of the system of Figure 1(a) can be obtained as

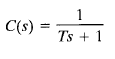
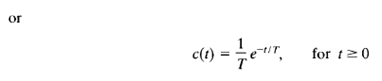
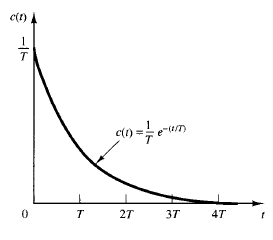
Fig: 2

The response curve given by the above equation is shown in Figure 2.

An important property of linear time-invariant systems:

 

In the analysis above, it has been shown that for the unit-ramp input the output c(t) is

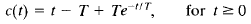
For the unit-step input, which is the derivative of unit-ramp input, the output c(t) is

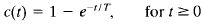
Finally, for the unit-impulse input, which is the derivative of unit-step input, the output c(t) is

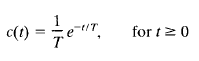
Comparison of the system responses to these three inputs clearly indicates that the response to the derivative of an input signal can be obtained by differentiating the response of the system to the original signal. It can also be seen that the response to the integral of the original signal can be obtained by integrating the response of the system to the original signal and by determining the integration constants from the zero output initial condition. This is a property of linear time-invariant systems. Linear time varying systems and nonlinear systems do not possess this property.