Ziegler-nichols First Method For Tuning Pid Controllers
Ziegler-Nichols first method for tuning PID controllers
Ziegler and Nichols proposed rules for determining values of the proportional gain Kp , integral time Ti, and derivative time Td based on the transient response characteristics of a given plant. Such determination of the parameters of PID controllers or tuning of PID controllers can be made by engineers on site by experiments on the plant. (Numerous tuning rules for PID controllers have been proposed since the Ziegler-Nichols proposal. They are available in the literature. Here, however, we introduce only the Ziegler-Nichols tuning rules.) There are two methods called Ziegler-Nichols tuning rules. In both methods, they aimed at obtaining 25% maximum overshoot in step response. (Fig 1)
First method:
In the first method, we obtain experimentally the response of the plant to a unit-step input, as shown in Figure 2. If the plant involves neither integrator(s) nor dominant complex-conjugate poles, then such a unit-step response curve may look like an S-shaped curve, as shown in Figure 3. (If the response does not exhibit an S-shaped curve, this method does not apply.) Such step-response curves may be generated experimentally or from a dynamic simulation of the plant.
The S-shaped curve may be characterized by two constants, delay time L and time constant T The delay time and time constant are determined by drawing a tangent line at the inflection point of the S-shaped curve and determining the intersections of the tangent line with the time axis and line e(t) = K, as shown in Figure 3. The transfer function C(s)/U(s) may then be approximated by a first-order system with a transport lag as follows:
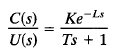
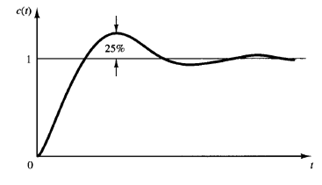
Fig: 1 Unit-step response curve showing 25% maximum over shoot Fig: 2Unit-step response of a plant
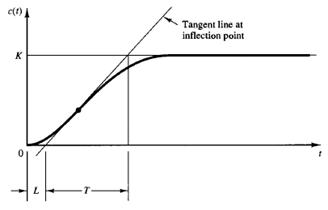
Fig: 3 S-shaped response curve
Ziegler and Nichols suggested to set the values of Kp, Ti , and Td according to the formula shown in Table 1.

Table 1: Ziegler-Nichols Tuning Rule Based on Step Response of Plant (First Method)
Notice that the PID controller tuned by the first method of Ziegler-Nichols rules gives
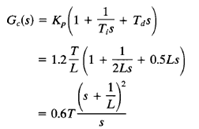
Thus, the PID controller has a pole at the origin and double zeros at S = -1/L.