Attribute-oriented Induction For Data Characterization
Introduction: The attribute-oriented induction (AOI) approach to concept description was first proposed in 1989, a few years before the introduction of the data cube approach. The data cube approach is essentially based on materialized views of the data, which typically have been pre-computed in a data warehouse. In general, it performs off-line aggregation before an OLAP or data mining query is submitted for processing. On the other hand, the attribute-oriented induction approach is basically a query-oriented, generalization-based, on-line data analysis technique. Note that there is no inherent barrier distinguishing the two approaches based on on-line aggregation versus off-line pre computation. Some aggregations in the data cube can be computed on-line, while off-line pre computation of multidimensional space can speed up attribute-oriented induction as well.
The general idea of attribute-oriented induction is to first collect the task-relevant data using a database query and then perform generalization based on the examination of the number of distinct values of each attribute in the relevant set of data.
The generalization is performed by either attribute removal or attribute generalization. Aggregation is performed by merging identical generalized tuples and accumulating their respective counts. This reduces the size of the generalized data set. The resulting generalized relation can be mapped into different forms for presentation to the user, such as charts or rules.
Example: Attribute-oriented induction. Here we show how attribute-oriented induction is performed on the initial working relation of Table 4.12. For each attribute of the relation, the generalization proceeds as follows:
1. name: Since there are a large number of distinct values for name and there is no generalization operation defined on it, this attribute is removed.
2. gender: Since there are only two distinct values for gender, this attribute is retained and no generalization is performed on it.
3. major: Suppose that a concept hierarchy has been defined that allows the attribute major to be generalized to the values farts& science, engineering, businessg. Suppose also that the attribute generalization threshold is set to 5, and that there are more than 20 distinct values for major in the initial working relation. By attribute generalization and attribute generalization control, major is therefore generalized by climbing the given concept hierarchy.
4. birth place: This attribute has a large number of distinct values; therefore, we would like to generalize it. Suppose that a concept hierarchy exists for birth place, defined as “city < province or state < country”. If the number of distinct values for country in the initial working relation is greater than the attribute generalization threshold, then birth place should be removed, because even though a generalization operator exists for it, the generalization threshold would not be satisfied. If instead, the number of distinct values for country is less than the attribute generalization threshold, then birth place should be generalized to birth country.
5. birth date: Suppose that a hierarchy exists that can generalize birth date to age, and age to age range, and that the number of age ranges (or intervals) is small with respect to the attribute generalization threshold. Generalization of birth date should therefore take place.
6. residence: Suppose that residence is defined by the attributes number, street, residence city, residence province or state, and residence country. The number of distinct values for number and street will likely be very high, since these concepts are quite low level. The attributes number and street should therefore be removed, so that residence is then generalized to residence city, which contains fewer distinct values.
7. phone#:As with the attribute name above, this attribute contains too many distinct values and should therefore be removed in generalization.
8. gpa: Suppose that a concept hierarchy exists for gpa that groups values for grade point average into numerical intervals like f3.75–4.0, 3.5–3.75,. . .g, which in turn are grouped into descriptive values, such as fexcellent, very good,. . .g. The attribute can therefore be generalized.
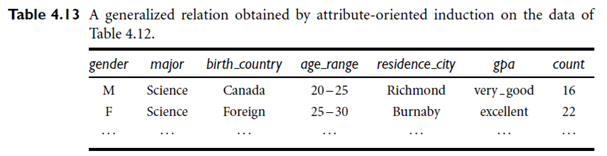
The generalization process will result in groups of identical tuples. For example, the first two tuples of Table 4.12 both generalize to the same identical tuple (namely, the first tuple shown in Table 4.13). Such identical tuples are then merged into one, with their counts accumulated. This process leads to the generalized relation shown in Table 4.13. Based on the vocabulary used in OLAP, we may view count as a measure, and the remaining attributes as dimensions. Note that aggregate functions, such as sum, may be applied to numerical attributes, like salary and sales. These attributes are referred to as measure attributes.
Implementation techniques and methods of presenting the derived generalization are discussed in the following subsections.