Classification Of Dynamic Data Streams
Introduction: Classification is a two-step process consisting of learning, or model construction (where a model is constructed based on class-labeled tuples from a training data set), and classification, or model usage (where the model is used to predict the class labels of tuples from new data sets). The latter lends itself to stream data, as new examples are immediately classified by the model as they arrive.
- In a traditional setting, the training data reside in a relatively static database. Many classification methods will scan the training data multiple times. Therefore, the first step of model construction is typically performed off-line as a batch process. With data streams, however, there is typically no off-line phase. The data flow in so quickly that storage and multiple scans are infeasible.
- To further illustrate how traditional classification methods are inappropriate for stream data; consider the practice of constructing decision trees as models. Most decision tree algorithms tend to follow the same basic top-down, recursive strategy, yet differ in the statistical measure used to choose an optimal splitting attribute. To review, a decision tree consists of internal (non leaf) nodes, branches, and leaf nodes. An attribute selection measure is used to select the splitting attribute for the current node. This is taken to be the attribute that best discriminates the training tuples according to class. In general, branches are grown for each possible value of the splitting attribute, the training tuples are partitioned accordingly, and the process is recursively repeated at each branch. However, in the stream environment, it is neither possible to collect the complete set of data nor realistic to rescan the data, thus such a method has to be re-examined.
- Another distinguishing characteristic of data streams is that they are time-varying, as opposed to traditional database systems, where only the current state is stored. This change in the nature of the data takes the form of changes in the target classification model over time and is referred to as concept drift. Concept drift is an important consideration when dealing with stream data.
- Several methods have been proposed for the classification of stream data. We introduce four of them in this subsection. The first three, namely the Hoeffding tree algorithm, Very Fast Decision Tree (VFDT), and Concept-adapting Very Fast Decision Tree (CVFDT), extend traditional decision tree induction. The fourth uses a classifier ensemble approach, in which multiple classifiers are considered using a voting method.
The Hoeffding tree algorithm is a decision tree learning method for stream data classification. It was initially used to track Web click streams and construct models to predict which Web hosts and Web sites a user is likely to access. It typically runs in sub linear time and produces a nearly identical decision tree to that of traditional batch learners. It uses Hoeffding trees, which exploit the idea that a small sample can often be enough to choose an optimal splitting attribute. This idea is supported mathematically by the Hoeffding bound (or additive Chernoff bound). Suppose we make N independent observations of a random variable r with range R, where r is an attribute selection measure. (For a probability, R is one, and for an information gain, it is log c, where c is the number of classes.) In the case of Hoeffding trees, r is information gain. If we compute the mean, r, of this sample, the Hoeffding bound states that the true mean of r is at least r-e, with probability 1-δ, where d is user-specified and
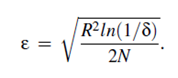
The Hoeffding tree algorithm uses the Hoeffding bound to determine, with high probability, the smallest number, N, of examples needed at a node when selecting a splitting attribute. This attribute would be the same as that chosen using infinite examples! We’ll see how this is done shortly. The Hoeffding bound is independent of the probability distribution, unlike most other bound equations. This is desirable, as it may be impossible to know the probability distribution of the information gain, or whichever attribute selection measure is used.
“How does the Hoeffding tree algorithm use the Hoeffding bound?” The algorithm takes as input a sequence of training examples, S, described by attributes A, and the accuracy parameter, d. In addition, the evaluation function G(Ai) is supplied, which could be information gain, gain ratio, Gini index, or some other attribute selection measure. At each node in the decision tree, we need to maximize G(Ai) for one of the remaining attributes, Ai. Our goal is to find the smallest number of tuples, N, for which the Hoeffding bound, is satisfied. For a given node, let Aa be the attribute that achieves the highest G, and Ab be the attribute that achieves the second highest G. If G (Aa)-G(Ab) > e, where e is calculated from Equation (8.4), we can confidently say that this difference is larger than zero. We select Aa as the best splitting attribute with confidence 1- δ.