Clique: A Dimension-growth Subspace Clustering Method

Introduction: CLIQUE (Clustering Inquest) was the first algorithm proposed for dimension-growth subspace clustering in high-dimensional space. In dimension-growth subspace clustering, the clustering process starts at single-dimensional subspaces and grows upward to higher-dimensional ones. Because CLIQUE partitions each dimension like a grid structure and determines whether a cell is dense based on the number of points it contains, it can also be viewed as an integration of density-based and grid-based clustering methods. However, its overall approach is typical of subspace clustering for high-dimensional space, and so it is introduced in this section.

The ideas of the CLIQUE clustering algorithm are outlined as follows.

• Given a large set of multidimensional data points, the data space is usually not uniformly occupied by the data points. CLIQUE’s clustering identifies the sparse and the “crowded” areas in space (or units), thereby discovering the overall distribution patterns of the data set.
• A unit is dense if the fraction of total data points contained in it exceeds an input model parameter. In CLIQUE, a cluster is defined as a maximal set of connected dense units.

CLIQUE performs multidimensional clustering in two steps.

In the first step, CLIQUE partitions the d-dimensional data space into non overlapping rectangular units, identifying the dense units among these. This is done (in 1-D) for each dimension. For example, Figure 7.21 shows dense rectangular units found with respect to age for the dimensions salary and (number of weeks of) vacation. The subspaces representing these dense units are intersected to form a candidate search space in which dense units of higher dimensionality may exist.

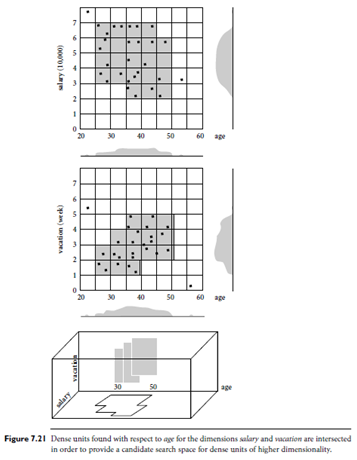CLIQUE confine its search for dense units of higher dimensionality to the intersection of the dense units in the subspaces: The identification of the candidate searchspace is based on the A priori property used in association rule mining.8 In general, theproperty employs prior knowledge of items in the search space so that portions of thespace can be pruned. The property, adapted for CLIQUE, states the following: If a k-dimensional unit is dense, then so are its projections in (k-1)-dimensional space. That is,given a k-dimensional candidate dense unit, if we check its (k-1)-th projection units andfind any that are not dense, then we know that the kth dimensional unit cannot be denseeither. Therefore, we can generate potential or candidate dense units in k-dimensionalspace from the dense units found in (k-1)-dimensional space. In general, the resultingspace searched is much smaller than the original space. The dense units are thenexamined in order to determine the clusters.

In the second step, CLIQUE generates a minimal description for each cluster as follows. For each cluster, it determines the maximal region that covers the cluster of connected dense units. It then determines a minimal cover (logic description) for each cluster.

CLIQUE automatically finds subspaces of the highest dimensionality such that high-density clusters exist in those subspaces. It is insensitive to the order of input objects and does not presume any canonical data distribution. It scales linearly with the size of input and has good scalability as the number of dimensions in the data is increased. However, obtaining meaningful clustering results is dependent on proper tuning of the grid size (which is a stable structure here) and the density threshold.

This is particularly difficult because the grid size and density threshold are used across all combinations of dimensions in the data set. Thus, the accuracy of the clustering results may be degraded at the expense of the simplicity of the method. Moreover, for a given dense region, all projections of the region onto lower-dimensionality subspaces will also be dense. This can result in a large overlap among the reported dense regions. Furthermore, it is difficult to find clusters of rather different density with in different dimensional subspaces.

Several extensions to this approach follow a similar philosophy. For example, let’s think of a grid as a set of fixed bins. Instead of using fixed bins for each of the dimensions, we can use an adaptive, data-driven strategy to dynamically determine the bins for each dimension based on data distribution statistics. Alternatively, instead of using a density threshold, we would use entropy as a measure of the quality of subspace clusters.