Clustering With Obstacle Objects

Introduction: Obstacles introduce constraints on the distance function. The straight-line distance between two points is meaningless if there is an obstacle in the way.

A partitioning clustering method is preferable because it minimizes the distance between objects and their cluster centers. If we choose the k-means method, a cluster center may not be accessible given the presence of obstacles. For example, the cluster mean could turn out to be in the middle of a lake. On the other hand, the k-medoids method chooses an object within the cluster as a center and thus guarantees that such a problem cannot occur. Recall that every time a new medoid is selected, the distance between eachobject and its newly selected cluster center has to be recomputed. Because there could be obstacles between two objects, the distance between two objects may have to be derived by geometric computations (e.g., involving triangulation). The computational cost can get very high if a large number of objects and obstacles are involved.

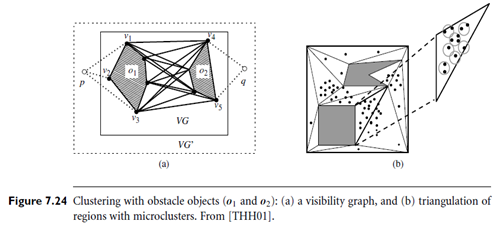
The clustering with obstacles problem can be represented using a graphical notation. First, a point, p, is visible from another point, q, in the region, R, if the straight line joining p and q does not intersect any obstacles. A visibility graph is the graph, VG = (V, E), such that each vertex of the obstacles has a corresponding node in V and two nodes, v1 and v2, in V are joined by an edge in E if and only if the corresponding vertices they represent are visible to each other. Let VG’ = (V’, E’) be a visibility graph created from VG by adding two additional points, p and q, in V’. E’ contains an edge joining two points in V’ if the two points are mutually visible. The shortest path between two points, p and q, will be a sub path of VG0 as shown in Figure 7.24(a). We see that it begins with an edge from p to either v1, v2, or v3, goes through some path in VG, and then ends with an edge from either v4 or v5 to q.

To reduce the cost of distance computation between any two pairs of objects or points, several preprocessing and optimization techniques can be used. One method groups points that are close together into micro clusters. This can be done by first triangulating the region R into triangles, and then grouping nearby points in the same triangle into micro clusters, using a method similar to BIRCH or DBSCAN, as shown in Figure 7.24(b). By processing micro clusters rather than individual points, the overall computation is reduced. After that, pre-computation can be performed to build two kinds of join indices based on the computation of the shortest paths: (1) VV indices, for any pair of obstacle vertices, and (2) MV indices, for any pair of micro cluster and obstacle vertex. Use of the indices helps further optimize the overall performance.

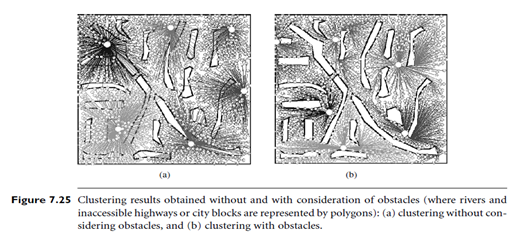
With such pre computation and optimization, the distance between any two points (at the granularity level of micro cluster) can be computed efficiently. Thus, the clustering process can be performed in a manner similar to a typical efficient k-medoids algorithm, such as CLARANS, and achieve good clustering quality for large data sets. Given a large set of points, Figure 7.25(a) shows the result of clustering a large set of points without considering obstacles, whereas Figure 7.25(b) shows the result with consideration of obstacles. The latter represents rather different but more desirable clusters. For example, if we carefully compare the upper left-hand corner of the two graphs, we see that Figure 7.25(a) has a cluster center on an obstacle (making the center inaccessible), whereas all cluster centers in Figure 7.25(b) are accessible. A similar situation has occurred with respect to the bottom right-hand corner of the graphs.