Conceptual Clustering

Introduction: Conceptual clustering is a form of clustering in machine learning that, given a set of unlabeled objects, produces a classification scheme over the objects. Unlike conventional clustering, which primarily identifies groups of like objects, conceptual clustering goes one step further by also finding characteristic descriptions for each group, where each group represents a concept or class. Hence, conceptual clustering is a two-step process: clustering is performed first, followed by characterization. Here, clustering quality is not solely a function of the individual objects. Rather, it incorporates factors such as the generality and simplicity of the derived concept descriptions.

• Most methods of conceptual clustering adopt a statistical approach that uses probability measurements in determining the concepts or clusters. Probabilistic descriptions are typically used to represent each derived concept.
• COBWEB is a popular and simple method of incremental conceptual clustering. Its input objects are described by categorical attribute-value pairs. COBWEB creates a hierarchical clustering in the form of a classification tree.
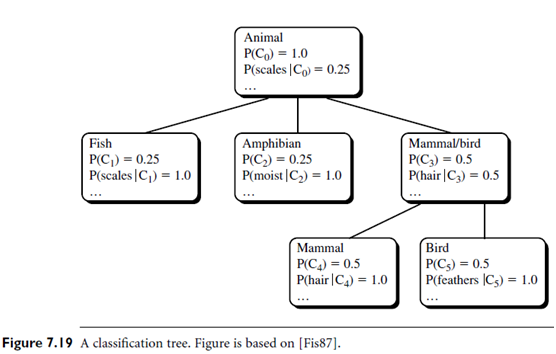
• “But what is a classification tree? Is it the same as a decision tree?” Figure 7.19 shows a classification tree for a set of animal data. A classification tree differs from a decision tree. Each node in a classification tree refers to a concept and contains a probabilistic description of that concept, which summarizes the objects classified under the node. The probabilistic description includes the probability of the concept and conditional probabilities of the form P(Ai = v_ij|C_k), where Ai = vij is an attribute-value pair (that is, the i^th attribute takes its j^th possible value) and Ck is the concept class. (Counts are accumulated and stored at each node for computation of the probabilities.) This is unlike decision trees, which label branches rather than nodes and use logical rather than probabilistic descriptors. The sibling nodes at a given level of a classification tree are said to form a partition. To classify an object using a classification tree, a partial matching function is employed to descend the tree along a path of “best” matching nodes.

COBWEB uses a heuristic evaluation measure called category utility to guide construction of the tree. Category utility (CU) is defined as

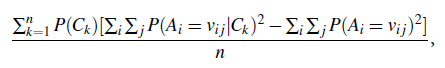
where n is the number of nodes, concepts, or “categories” forming a partition, {C1, C2, : : : , Cn}, at the given level of the tree. In other words, category utility is the increase in the expected number of attribute values that can be correctly guessed given a partition (where this expected number corresponds to the term P(Ck) ΣiΣj P(Ai = vij|Ck)²) over the expected number of correct guesses with no such knowledge (corresponding to the term ΣiΣjP(Ai = vij)²). Although we do not have room to show the derivation, category utility rewards intra class similarity and interclass dissimilarity, where:

Intra class similarity is the probability P (Ai = vij|Ck). The larger this value is, the greater the proportion of class members that share this attribute-value pair and the more predictable the pair is of class members.

Interclass dissimilarity is the probability P (Ck|Ai = vij). The larger this value is, the fewer the objects in contrasting classes that share this attribute-value pair and the more predictive the pair is of the class.