Data Transformation

Introduction: In data transformation, the data are transformed or consolidated into forms appropriate for mining. Data transformation can involve the following:

• Smoothing, which works to remove noise from the data. Such techniques include binning, regression, and clustering.
• Aggregation, where summary or aggregation operations are applied to the data. For example, the daily sales data may be aggregated so as to compute monthly and annual total amounts. This step is typically used in constructing a data cube for analysis of the data at multiple granularities.
• Generalization of the data, where low-level or “primitive” (raw) data are replaced by higher-level concepts through the use of concept hierarchies. For example, categorical   attributes, like street, can be generalized to higher-level concepts, like city or country. Similarly, values for numerical attributes, like age, may be mapped to higher-level concepts, like youth, middle-aged, and senior.
• Normalization, where the attribute data are scaled so as to fall within a small specified range, such as 1:0 to 1:0, or 0:0 to 1:0.
• Attribute construction (or feature construction), where new attributes are constructed and added from the given set of attributes to help the mining process.

Smoothing is a form of data cleaning and was addressed in Section 2.3.2. Section 2.3.3 on the data cleaning process also discussed ETL tools, where users specify transformations to correct data inconsistencies. Aggregation and generalization serve as forms of data reduction and are discussed in Sections 2.5 and 2.6, respectively. In this section, we therefore discuss normalization and attribute construction.

An attribute is normalized by scaling its values so that they fall within a small specified range, such as 0.0 to 1.0.Normalization is particularly useful for classification algorithms involving neural networks, or distance measurements such as nearest-neighbor classification and clustering. If using the neural network back propagation algorithm for classification mining (Chapter 6), normalizing the input values for each attribute measured in the training tuples will help speed up the learning phase. For distance-based methods, normalization helps prevent attributes with initially large ranges (e.g., income) from out weighing attributes with initially smaller ranges (e.g., binary attributes). There are many methods for data normalization. We study three: min-max normalization, z-score normalization, and normalization by decimal scaling.

Min-max normalization performs a linear transformation on the original data. Suppose that minA and maxA are the minimum and maximum values of an attribute, A. Min-max normalization maps a value, v, of A to v0 in the range [new_minA; new_maxA] by computing

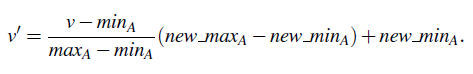
Min-max normalization preserves the relationships among the original data values. It will encounter an “out-of-bounds” error if a future input case for normalization falls outside of the original data range for A.

Example: Decimal scaling. Suppose that the recorded values of A range from _986 to 917. The maximum absolute value of A is 986. To normalize by decimal scaling, we therefore divide each value by 1,000 (i.e., j = 3) so that _986 normalizes to _0:986 and 917 normalizes to 0:917.

Note that normalization can change the original data quite a bit, especially the latter two methods shown above. It is also necessary to save the normalization parameters (such as the mean and standard deviation if using z-score normalization) so that future data can be normalized in a uniform manner.

In attribute construction,5 new attributes are constructed from the given attributes and added in order to help improve the accuracy and understanding of structure in high-dimensional data. For example, we may wish to add the attribute area based on the attributes height and width. By combining attributes, attribute construction can discover missing information about the relationships between data attributes that can be useful for knowledge discovery.