Evaluating The Accuracy Of A Classifier Or Predictor

Introduction: How can we use the above measures to obtain a reliable estimate of classifier accuracy (or predictor accuracy in terms of error)? Holdout, random sub sampling, cross validation, and the bootstrap are common techniques for assessing accuracy based on randomly sampled partitions of the given data. The use of such techniques to estimate accuracy increases the overall computation time, yet is useful for model selection.

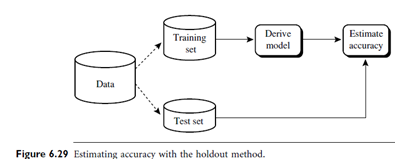
Holdout Method and Random Sub sampling: The holdout method is what we have alluded to so far in our discussions about accuracy. In this method, the given data are randomly partitioned into two independent sets, a training set and a test set. Typically, two-thirds of the data are allocated to the training set, and the remaining one-third is allocated to the test set. The training set is used to derive the model, whose accuracy is estimated with the test set (Figure 6.29). The estimate is pessimistic because only a portion of the initial data is used to derive the model.

Random sub sampling is a variation of the holdout method in which the holdout method is repeated k times. The overall accuracy estimate is taken as the average of the accuracies obtained from each iteration. (For prediction, we can take the average of the predictor error rates.)

Cross-validation: In k-fold cross-validation, the initial data are randomly partitioned into k mutually exclusive subsets or “folds,” D1, D2, …… , Dk, each of approximately equal size. Training and testing is performed k times. In iteration i, partition Di is reserved as the test set, and the remaining partitions are collectively used to train the model. That is, in the first iteration, subsets D2,… , Dk collectively serve as the training set in order to obtain a first model, which is tested on D1; the second iteration is trained on subsets D1, D3, …. , Dk and tested on D2; and so on. Unlike the holdout and random sub sampling methods above, here, each sample is used the same number of times for training and once for testing. For classification, the accuracy estimate is the overall number of correct classifications from the k iterations, divided by the total number of tuples in the initial data. For prediction, the error estimate can be computed as the total loss from the k iterations, divided by the total number of initial tuples.

Leave-one-out is a special case of k-fold cross-validation where k is set to the number of initial tuples. That is, only one sample is “left out” at a time for the test set. In stratified cross-validation, the folds are stratified so that the class distribution of the tuples in each fold is approximately the same as that in the initial data.

In general, stratified 10-fold cross-validation is recommended for estimating accuracy (even if computation power allows using more folds) due to its relatively low bias and variance.

Bootstrap: Unlike the accuracy estimation methods mentioned above, the bootstrap method samples the given training tuples uniformly with replacement. That is, each time a tuple is selected, it is equally likely to be selected again and readded to the training set. For instance, imagine a machine that randomly selects tuples for our training set. In sampling with replacement, the machine is allowed to select the same tuple more than once.

There are several bootstrap methods. A commonly used one is the .632 bootstrap, which works as follows. Suppose we are given a data set of d tuples. The data set is sampled d times, with replacement, resulting in a bootstrap sample or training set of d samples. It is very likely that some of the original data tuples will occur more than once in this sample. The data tuples that did not make it into the training set end up forming the test set.