Forward Algorithm

ntroduction: What is the probability, P(x), that sequence x was generated by a given hidden Markov model. This problem can be solved using the forward algorithm. Let x = x1,x2 : : : xL be our sequence of symbols. A path is a sequence of states. Many paths can generate x. Consider one such path, which we denote π = π1π2 . . . . . πL. If we incorporate the begin and end states, denoted as 0, we can write π as π₀ = 0, π₁π₂ . . . . .  π_L, π_{L 1} = 0. The probability that the model generated sequence x using path p is

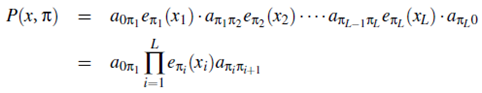
Where pL 1 = 0.We must, however, consider all of the paths that can generate x. Therefore, the probability of x given the model is

P(x) =åpP(x, p)

That is, we add the probabilities of all possible paths for x.

Algorithm:Forward algorithm. Find the probability, P(x), that sequence x was generated by the given hidden Markov model.

Input:

• A hidden Markov model, defined by a set of states, Q, that emit symbols, and by transition and emission probabilities;
• x, a sequence of symbols.

Output:Probability, P(x).

Method:

(1)Initialization(i = 0): f₀(0) = 1, f_k(0) = 0 for k > 0

(2) Recursion(i = 1: : :L): f_l (i) = e_l (xi)å_kf_k(i-1)a_kl

(3) Termination: P(x) = å_kf_k(L)a_k0

Unfortunately, the number of paths can be exponential with respect to the length, L, of x, so brute force evaluation by enumerating all paths is impractical. The forward algorithm exploits a dynamic programming technique to solve this problem. It defines forward variables, f_k(i), to be the probability of being in state k having observed the first i symbols of sequence x. We want to compute fpL 1=0 (L), the probability of being in the end state having observed all of sequence x.

The forward algorithm is shown above. It consists of three steps. In step 1, the forward variables are initialized for all states. Because we have not viewed any part of the sequence at this point, the probability of being in the start state is 1 (i.e., f₀(0) = 1), and the probability of being in any other state is 0. In step 2, the algorithm sums over all the probabilities of all the paths leading from one state emission to another. It does this recursively for each move from state to state. Step 3 gives the termination condition. The whole sequence (of length L) has been viewed, and we enter the end state, 0.We end up with the summed-over probability of generating the required sequence of symbols.