Hierarchical Methods
Introduction: A hierarchical clustering method works by grouping data objects into a tree of clusters. Hierarchical clustering methods can be further classified as either agglomerative or divisive, depending on whether the hierarchical decomposition is formed in a bottom-up (merging) or top-down (splitting) fashion. The quality of a pure hierarchical clustering method suffers from its inability to perform adjustment once a merge or split decision has been executed. That is, if a particular merge or split decision later turns out to have been a poor choice, the method cannot backtrack and correct it. Recent studies have emphasized the integration of hierarchical agglomeration with iterative relocation methods.
Agglomerative and Divisive Hierarchical Clustering
In general, there are two types of hierarchical clustering methods:
- Agglomerative hierarchical clustering: This bottom-up strategy starts by placing each object in its own cluster and then merges these atomic clusters into larger and larger clusters, until all of the objects are in a single cluster or until certain termination conditions are satisfied. Most hierarchical clustering methods belong to this category. They differ only in their definition of inter cluster similarity.
- Divisive hierarchical clustering: This top-down strategy does the reverse of agglomerative hierarchical clustering by starting with all objects in one cluster. It subdivides the cluster into smaller and smaller pieces, until each object forms a cluster on its own or until it satisfies certain termination conditions, such as a desired number of clusters is obtained or the diameter of each cluster is within a certain threshold.
BIRCH: Balanced Iterative Reducing and Clustering Using Hierarchies
BIRCH is designed for clustering a large amount of numerical data by integration of hierarchical clustering (at the initial micro clustering stage) and other clustering methods such as iterative partitioning (at the later macro clustering stage). It overcomes the two difficulties of agglomerative clustering methods: (1) scalability and (2) the inability to undo what was done in the previous step.
BIRCH introduces two concepts, clustering feature and clustering feature tree (CF tree), which are used to summarize cluster representations. These structures help theclustering method achieve good speed and scalability in large databases and also make iteffective for incremental and dynamic clustering of incoming objects.Let’s look closer at the above-mentioned structures. Given n d-dimensional dataobjects or points in a cluster, we can define the centroid x0, radius R, and diameter D of the cluster as follows:
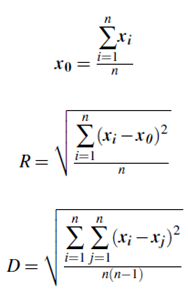
where R is the average distance from member objects to the centroid, and D is the average pair wise distance within a cluster. Both R and D reflect the tightness of the cluster around the centroid. A clustering feature (CF) is a three-dimensional vector summarizing information about clusters of objects. Given n d-dimensional objects or points in a cluster, {xi}, then the CF of the cluster is defined as
CF = (n, LS, SS),
where n is the number of points in the cluster, LS is the linear sum of the n points (i.e., Σni=1xi2), and SS is the square sum of the data points (i.e., Σni =1xi2).
A clustering feature is essentially a summary of the statistics for the given cluster: the zeroth, first, and second moments of the cluster from a statistical point of view. Clustering features are additive. For example, suppose that we have two disjoint clusters, C1 and C2, having the clustering features, CF1 and CF2, respectively. The clustering feature for the cluster that is formed by merging C1 and C2 is simply CF1 CF2.
Clustering features are sufficient for calculating all of the measurements that are needed for making clustering decisions in BIRCH. BIRCH thus utilizes storage efficiently by employing the clustering features to summarize information about the clusters of objects, thereby bypassing the need to store all objects.