Ilp Approach To Multi-relational Classification

Introduction: Inductive Logic Programming (ILP) is the most widely used category of approaches to multi relational classification. There are many ILP approaches. In general, they aim to find hypotheses of a certain format that can predict the class labels of target tuples, based on background knowledge (i.e., the information stored in all relations). The ILP problem is defined as follows: Given background knowledge B, a set of positive examples P, and a set of negative examples N, find a hypothesis H such that: (1) 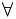t ∈ P : H∪B |=t (completeness), and (2) 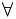t ∈ N : H ∪B ≠t (consistency), where |= stands for logical implication.

Well-known ILP systems include FOIL, Golem, and Progol. FOIL is a top-down learner, which builds rules that cover many positive examples and few negative ones. Golem is a bottom-up learner, which performs generalizations from the most specific rules. Progol uses a combined search strategy. Recent approaches, like TILDE, Mr- SMOTI, and RPTs, use the idea of C4.5 and inductively construct decision trees from relational data.

Although many ILP approaches achieve good classification accuracy, most of them are not highly scalable with respect to the number of relations in the database. The target relation can usually join with each non target relation via multiple join paths. Thus, in a database with reasonably complex schema, a large number of join paths will need to be explored. In order to identify good features, many ILP approaches repeatedly join the relations along different join paths and evaluate features based on the joined relation. This is time consuming, especially when the joined relation contains many more tuples than the target relation.

We look at FOIL as a typical example of ILP approaches. FOIL is a sequential covering algorithm that builds rules one at a time. After building a rule, all positive target tuples satisfying that rule are removed, and FOIL will focus on tuples that have not been covered by any rule. When building each rule, predicates are added one by one. At each step, every possible predicate is evaluated, and the best one is appended to the current rule.

To evaluate a predicate p, FOIL temporarily appends it to the current rule. This forms the rule r p. FOIL constructs a new data set, which contains all target tuples satisfying r p, together with the relevant non target tuples on the join path specified by r p. Predicate p is evaluated based on the number of positive and negative target tuples satisfying r p, using the foil gain measure, which is defined as follows: Let P(r) and N(r) denote the number of positive and negative tuples satisfying a rule r, respectively. Suppose the current rule is r. The foil gain of p is computed as follows:

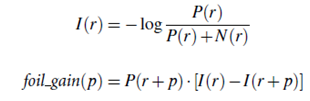
Intuitively, foil_gain (p) represents the total number of bits saved in representing positive tuples by appending p to the current rule. It indicates how much the predictive power of the rule can be increased by appending p to it. The best predicate found is the one with the highest foil gain.