Mining Multidimensional Association Rules

Introduction:

Using Static Discretization of Quantitative Attributes: Quantitative attributes, in this case, are discretized before mining using predefined concept hierarchies or data discretization techniques, where numeric values are replaced by interval labels. Categorical attributes may also be generalized to higher conceptual levels if desired.

 If the resulting task-relevant data are stored in a relational table, then any of the frequent itemset mining algorithms we have discussed can be modified easily so as to find all frequent predicate sets rather than frequent itemsets. In particular, instead of searching on only one attribute like buys, we need to search through all of the relevant attributes, treating each attribute-value pair as an itemset.

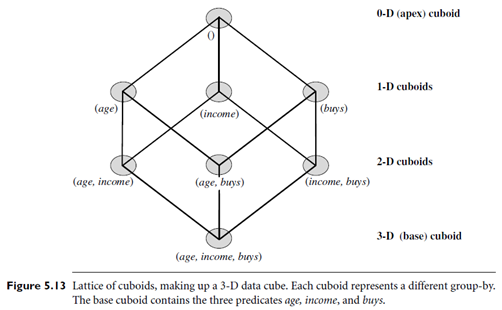Alternatively, the transformed multidimensional data may be used to construct a data cube. Data cubes are well suited for the mining of multidimensional association rules: They store aggregates (such as counts), in multidimensional space, which is essential for computing the support and confidence of multidimensional association rules. The cells of an n-dimensional cuboid can be used to store the support counts of the corresponding n-predicate sets. The base cuboid aggregates the task-relevant data by age, income, and buys; the 2-D cuboid, (age, income), aggregates by age and income, and so on; the 0-D (apex) cuboid contains the total number of transactions in the task-relevant data.

Due to the ever-increasing use of data warehouse and OLAP technology, it is possible that a data cube containing the dimensions that are of interest to the user may already exist, fully materialized. If this is the case, we can simply fetch the corresponding aggregate values and return the rules needed using a rule generation algorithm (Section 5.2.2). Notice that even in this case, the Apriori property can still be used to prune the search space. If a given k-predicate set has support sup, which does not satisfy minimum support, then further exploration of this set should be terminated. This is because any more specialized version of the k-itemset will have support no greater that sup and, therefore, will not satisfy minimum support either. In cases where no relevant data cube exists for the mining task, we must create one on the fly. This becomes an iceberg cube computation problem, where the minimum support threshold is taken as the iceberg condition.