Ratio-scaled Variables
Introduction: A ratio-scaled variable makes a positive measurement on a nonlinear scale, such as an exponential scale, approximately following the formula
AeBt or Ae-Bt
where A and B are positive constants, and t typically represents time. Common examples include the growth of a bacteria population or the decay of a radioactive element.
There are three methods to handle ratio-scaled variables for computing the dissimilarity between objects.
- Treat ratio-scaled variables like interval-scaled variables. This, however, is not usually a good choice since it is likely that the scale may be distorted.
- Apply logarithmic transformation to a ratio-scaled variable f having value xif for object i by using the formula yif = log (xif ). The yif values can be treated as interval valued, as described in Section 7.2.1. Notice that for some ratio-scaled variables, log-log or other transformations may be applied, depending on the variable’s definition and the application.
- Treat xi f as continuous ordinal data and treat their ranks as interval-valued.
The latter two methods are the most effective, although the choice of method used may depend on the given application.
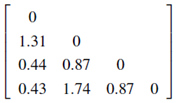
Example: Dissimilarity between ratio-scaled variables. This time, we have the sample data of Table 7.3, except that only the object-identifier and the ratio-scaled variable, test-3, are available. Let’s try a logarithmic transformation. Taking the log of test-3 results in the values 2.65, 1.34, 2.21, and 3.08 for the objects 1 to 4, respectively. Using the Euclidean distance (Equation (7.5)) on the transformed values, we obtain the following dissimilarity matrix: