Representative Object-based Technique
The k-Medoids Method: The k-means algorithm is sensitive to outliers because an object with an extremely large value may substantially distort the distribution of data. This effect is particularly exacerbated due to the use of the square-error function.
“How might the algorithm be modified to diminish such sensitivity?” Instead of taking the mean value of the objects in a cluster as a reference point, we can pick actual objects to represent the clusters, using one representative object per cluster. Each remaining object is clustered with the representative object to which it is the most similar. The partitioning method is then performed based on the principle of minimizing the sum of the dissimilarities between each object and its corresponding reference point. That is, an absolute-error criterion is used, defined as
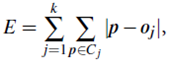
where E is the sum of the absolute error for all objects in the data set; p is the point in space representing a given object in cluster Cj; and oj is the representative object of Cj. In general, the algorithm iterates until, eventually, each representative object is actually the medoid, or most centrally located object, of its cluster. This is the basis of the k-medoids method for grouping n objects into k clusters.
Let’s look closer at k-medoids clustering. The initial representative objects (or seeds) are chosen arbitrarily. The iterative process of replacing representative objects by non representative objects continues as long as the quality of the resulting clustering is improved. This quality is estimated using a cost function that measures the average dissimilarity between an object and the representative object of its cluster. To determine whether a non representative object, orandom, is a good replacement for a current representative object, oj, the following four cases are examined for each of the non representative objects, p, as illustrated in Figure 7.4.
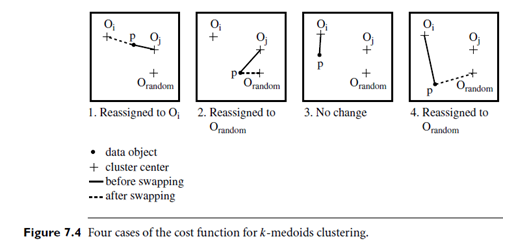
Case 1: p currently belongs to representative object, oj. If oj is replaced by orandom as a representative object and p is closest to one of the other representative objects, oi, i ≠ j, then p is reassigned to oi.
Case 2: p currently belongs to representative object, oj. If oj is replaced by orandom as a representative object and p is closest to orandom, then p is reassigned to orandom.
Case 3: p currently belongs to representative object, oi, i ≠ j. If oj is replaced by orandom as a representative object and p is still closest to oi, then the assignment does not change.
Case 4: p currently belongs to representative object, oi, i ≠ j. If oj is replaced by orandom as a representative object and p is closest to orandom, then p is reassigned to orandom.
Algorithm: k-medoids. PAM, a k-medoids algorithm for partitioning based on medoid or central objects.
Input:
- k: the number of clusters,
- D: a data set containing n objects.
- Output: A set of k clusters.
Method:
(1) arbitrarily choose k objects in D as the initial representative objects or seeds;
(2) repeat
(3) assign each remaining object to the cluster with the nearest representative object;
(4) randomly select a non-representative object, orandom;
(5) compute the total cost, S, of swapping representative object, oj, with orandom;
(6) if S < 0 then swap oj with orandom to form the new set of k representative objects;
(7) until no change;