Types Of Data In Cluster Analysis

Introduction: In this section, we study the types of data that often occur in cluster analysis and how to preprocess them for such an analysis. Suppose that a data set to be clustered contains n objects, which may represent persons, houses, documents, countries, and so on.

Main memory-based clustering algorithms typically operate on either of the following two data structures.

Data matrix (or object-by-variable structure): This represents n objects, such as persons, with p variables (also called measurements or attributes), such as age, height, weight, gender, and so on. The structure is in the form of a relational table, or n-by-p matrix (n objects X p variables):

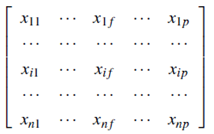
Dissimilarity matrix (or object-by-object structure): This stores a collection of proximities that are available for all pairs of n objects. It is often represented by an n-by-n table:

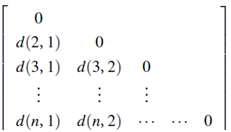
where d(i, j) is the measured difference or dissimilarity between objects i and j. In general, d(i, j) is a nonnegative number that is close to 0 when objects i and j are highly similar or “near” each other, and becomes larger the more they differ. Since d(i, j)=d( j, i), and d(i, i)=0, we have the matrix in (7.2).Measures of dissimilarity are discussed throughout this section.

The rows and columns of the data matrix represent different entities, while those of the dissimilarity matrix represent the same entity. Thus, the data matrix is often called a two-mode matrix, whereas the dissimilarity matrix is called a one-mode matrix. Many clustering algorithms operate on a dissimilarity matrix. If the data are presented in the form of a data matrix, it can first be transformed into a dissimilarity matrix before applying such clustering algorithms.

In this section, we discuss how object dissimilarity can be computed for objects described by interval-scaled variables; by binary variables; by categorical, ordinal, and ratio-scaled variables; or combinations of these variable types. Non metric similarity between complex objects (such as documents) is also described. The dissimilarity data can later be used to compute clusters of objects.