Wave Cluster: Clustering Using Wavelet Transformation

Introduction: Wave Cluster is a multiresolution clustering algorithm that first summarizes the data by imposing a multidimensional grid structure onto the data space. It then uses a wavelet transformation to transform the original feature space, finding dense regions in the transformed space.

In this approach, each grid cell summarizes the information of a group of points that map into the cell. This summary information typically fits into main memory for use by the multiresolution wavelet transform and the subsequent cluster analysis. A wavelet transform is a signal processing technique that decomposes a signal into different frequency sub bands. The wavelet model can be applied to d-dimensional signals by applying a one-dimensional wavelet transforms d times. In applying a wavelet transform, data are transformed so as to preserve the relative distance between objects at different levels of resolution. This allows the natural clusters in the data to become more distinguishable. Clusters can then be identified by searching for dense regions in the new domain. Additional references to the technique are given in the bibliographic notes.

Wavelet transformation offers the following advantages:

It provides unsupervised clustering. It uses hat-shaped filters that emphasize regions where the points cluster, while suppressing weaker information outside of the cluster boundaries. Thus, dense regions in the original feature space act as attractors for nearby points and as inhibitors for points that are further away. This means that the clusters in the data automatically stand out and “clear” the regions around them. Thus, another advantage is that wavelet transformation can automatically result in the removal of outliers.

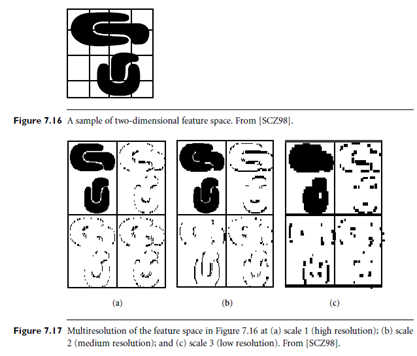
The multiresolution property of wavelet transformations can help detect clusters at varying levels of accuracy. For example, Figure 7.16 shows a sample of two dimensional feature space, where each point in the image represents the attribute or feature values of one object in the spatial data set. Figure 7.17 shows the resulting wavelet transformation at different resolutions, from a fine scale (scale 1) to a coarse scale (scale 3). At each level, the four sub bands into which the original data are decomposed are shown. The sub band shown in the upper-left quadrant emphasizes the average neighborhood around each data point. The sub band in the upper-right quadrant emphasizes the horizontal edges of the data. The sub band in the lower-left quadrant emphasizes the vertical edges, while the sub band in the lower-right quadrant emphasizes the corners.

Wavelet-based clustering is very fast, with a computational complexity of O(n), where n is the number of objects in the database. The algorithm implementation can be made parallel.

Wave Cluster is a grid-based and density-based algorithm. It conforms too many of the requirements of a good clustering algorithm: It handles large data sets efficiently, discovers clusters with arbitrary shape, successfully handles outliers, is insensitive to the order of input, and does not require the specification of input parameters such as the number of clusters or a neighborhood radius. In experimental studies, Wave Cluster was found to outperform BIRCH, CLARANS, and DBSCAN in terms of both efficiency and clustering quality. The study also found Wave Cluster capable of handling data with up to 20 dimensions.