Aggregate Analysis

Figure 17.2: An 8-bit binary counter as its value goes from 0 to 16 by a sequence of 16 INCREMENT operations. Bits that flip to achieve the next value are shaded. The running cost for flipping bits is shown at the right. Notice that the total cost is never more than twice the total number of INCREMENT operations.

As with the stack example, a cursory analysis yields a bound that is correct but not tight. A single execution of INCREMENT takes time Θ(k) in the worst case, in which array A contains all ′s. Thus, a sequence of n INCREMENT operations on an initially zero counter takes time O(nk) in the worst case.

We can tighten our analysis to yield a worst-case cost of O(n) for a sequence of n INCREMENT's by observing that not all bits flip each time INCREMENT is called. As Figure 17.2 shows, A[0] does flip each time INCREMENT is called. The next-highest-order bit, A[1], flips only every other time: a sequence of n INCREMENT operations on an initially zero counter causes A[1] to flip ⌈n/2⌉ times. Similarly, bit A[2] flips only every fourth time, or ⌈n/4⌉ times in a sequence of n INCREMENT's. In general, for i = 0, 1, ..., ⌈lg n⌉, bit A[i] flips ⌈n/2ⁱ⌉ times in a sequence of n INCREMENT operations on an initially zero counter. For i > ⌈lg n⌉, bit A[i] never flips at all. The total number of flips in the sequence is thus

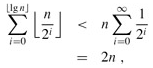
The worst-case time for a sequence of n INCREMENT operations on an initially zero counter is therefore O(n). The average cost of each operation, and therefore the amortized cost per operation, is O(n)/n = O(1).