Analysis Of Union By Rank With Path Compression
Analysis of union by rank with path compression: As noted in Disjoint-set forests, the running time of the combined union-by-rank and path-compression heuristic is O(m α (n)) for m disjoint-set operations on n elements. In this section, we shall examine the function α to see just how slowly it grows. Then we prove this running time using the potential method of amortized analysis.
A very quickly growing function and its very slowly growing inverse
For integers k ≥ 0 and j ≥ 1, we define the function Ak(j) as
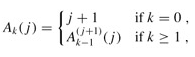
where the expression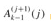 
uses the functional-iteration notation given in Standard notations and common functions Specifically, 
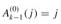and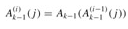 
for i ≥ 1. We will refer to the parameter k as the level of the function A.
The function Ak(j) strictly increases with both j and k. To see just how quickly this function grows, we first obtain closed-form expressions for A1(j) and A2(j).
For any integer j ≥ 1, we have A1(j) = 2 j 1.
Proof We first use induction on i to show that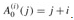 
. For the base case, we have 
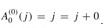. For the inductive step, assume that 
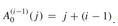. Then 
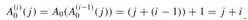. Finally, we note that 
.
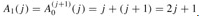For any integer j ≥ 1, we have A2(j) = 2j 1(j 1) - 1.
Proof We first use induction on i to show that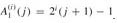 
. For the base case, we have 
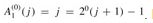. For the inductive step, assume that 
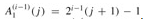. Then 
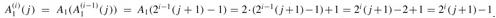. Finally, we note that 
.
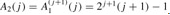Now we can see how quickly Ak(j) grows by simply examining Ak (1) for levels k = 0, 1, 2, 3, 4. From the definition of A0(k) and the above lemmas, we have A0(1) = 1 1 = 2, A1(1) = 2 · 1 1 = 3, and A2(1) = 21 1 · (1 1) - 1 = 7. We also have
| A3(1) | = |
 |
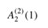| = | A2(A2(1)) | |
| = | A2(7) | |
| = | 28 · 8 - 1 | |
| = | 211 - 1 | |
| = | 2047 |
and
| A4(1) | = |
 |
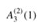| = | A3(A3(1)) | |
| = | A3(2047) | |
| = |
 |
|
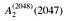| ≫ | A2(2047) | |
| = | 12048· 2048 - 1 | |
| > | 22048 | |
| = | (24)512 | |
| = | 16512 | |
| ≫ | 1080, |