Assembly-line Scheduling

Figure 15.2(b) shows the fi[j] values for the example of part (a), as computed by equations (15.6) and (15.7), along with the value of f*.
The fi[j] values give the values of optimal solutions to subproblems. To help us keep track of how to construct an optimal solution, let us define li [j] to be the line number, 1 or 2, whose station j - 1 is used in a fastest way through station Si,j . Here, i = 1, 2 and j = 2, 3, ..., n. (We avoid defining li[1] because no station precedes station 1 on either line.) We also define l* to be the line whose station n is used in a fastest way through the entire factory. The li[j] values help us trace a fastest way. Using the values of l* and li[j] shown in Figure 15.2(b), we would trace a fastest way through the factory shown in part (a) as follows. Starting with l* = 1, we use station S1,6. Now we look at l1[6], which is 2, and so we use station S2,5. Continuing, we look at l2[5] = 2 (use station S2,4), l2[4] = 1 (station S1,3), l1[3] = 2 (station S2,2), and l2[2] = 1 (station S1,1).
Step 3: Computing the fastest times
At this point, it would be a simple matter to write a recursive algorithm based on equation (15.1) and the recurrences (15.6) and (15.7) to compute the fastest way through the factory. There is a problem with such a recursive algorithm: its running time is exponential in n. To see why, let ri(j) be the number of references made to fi[j] in a recursive algorithm. From equation (15.1), we have
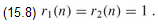
From the recurrences (15.6) and (15.7), we have
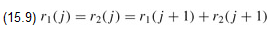
for j = 1, 2, ..., n - 1. As Exercise 15.1-2 asks you to show, ri(j) = 2n-j. Thus, f1[1] alone is referenced 2n-1 times! As Exercise 15.1-3 asks you to show, the total number of references to all fi[j] values is Θ(2n).
We can do much better if we compute the fi[j] values in a different order from the recursive way. Observe that for j ≥ 2, each value of fi[j] depends only on the values of f1[j - 1] and f2[j - 1]. By computing the fi[j] values in order of increasing station numbers j-left to right in Figure 15.2(b)-we can compute the fastest way through the factory, and the time it takes, in Θ(n) time. The FASTEST-WAY procedure takes as input the values ai,j, ti,j, ei, and xi , as well as n, the number of stations in each assembly line.
FASTEST-WAY(a, t, e, x, n) 1 f1[1] ← e1 a1,1 2 f2[1] ←e2 a2,1 3 for j ← 2 to n 4 do if f1[j - 1] a1,j ≤ f2[j - 1] t2,j-1 a1,j 5 then f1[j] ← f1[j - 1] a1, j 6 l1[j] ← 1 7 else f1[j] ← f2[j - 1] t2,j-1 a1,j 8 l1[j] ← 2 9 if f2[j - 1] a2,j ≤ f1[j - 1] t1,j-1 a2,j 10 then f2[j] ← f2[j - 1] a2,j 11 l2[j] ← 2 12 else f2[j] ∞ f1[j - 1] t1,j-1 a2,j 13 l2[j] ← 1 14 if f1[n] x1 ≤ f2[n] x2 15 then f* = f1[n] x1 16 l* = 1 17 else f* = f2[n] x2 18 l* = 2