Asymptotic Notation In Equations And Inequalities
Asymptotic notation in equations and inequalities: We have already seen how asymptotic notation can be used within mathematical formulas. For example, in introducing O-notation, we wrote "n = O(n2)." We might also write 2n2 3n 1 = 2n2 Θ(n). How do we interpret such formulas?
When the asymptotic notation stands alone on the right-hand side of an equation (or inequality), as in n = O(n2), we have already defined the equal sign to mean set membership: n ∈O(n2). In general, however, when asymptotic notation appears in a formula, we interpret it as standing for some anonymous function that we do not care to name. For example, the formula 2n2 3n 1 = 2n2 Θ(n) means that 2n2 3n 1 = 2n2 f(n), where f(n) is some function in the set Θ(n). In this case, f(n) = 3n 1, which indeed is in Θ(n).
Using asymptotic notation in this manner can help eliminate inessential detail and clutter in an equation. For example, in Chapter 2 we expressed the worst-case running time of merge sort as the recurrence
T(n) = 2T (n/2) Θ(n).
If we are interested only in the asymptotic behavior of T(n), there is no point in specifying all the lower-order terms exactly; they are all understood to be included in the anonymous function denoted by the term Θ(n).
The number of anonymous functions in an expression is understood to be equal to the number of times the asymptotic notation appears. For example, in the expression
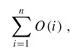
there is only a single anonymous function (a function of i). This expression is thus not the same as O(1) O(2) . . . O(n), which doesn't really have a clean interpretation.
In some cases, asymptotic notation appears on the left-hand side of an equation, as in
2n2 Θ(n) = Θ(n2).
We interpret such equations using the following rule: No matter how the anonymous functions are chosen on the left of the equal sign, there is a way to choose the anonymous functions on the right of the equal sign to make the equation valid. Thus, the meaning of our example is that for any function f(n) ∈Θ(n), there is some function g(n) ∈Θ(n2) such that 2n2 f(n) = g(n) for all n. In other words, the right-hand side of an equation provides a coarser level of detail than the left-hand side.
A number of such relationships can be chained together, as in
2n2 3n 1 = 2n2 Θ(n) = Θ(n2).
We can interpret each equation separately by the rule above. The first equation says that there is some function f(n) ∈Θ(n) such that 2n2 3n 1 = 2n2 f(n) for all n. The second equation says that for any function g(n) ∈Θ(n) (such as the f(n) just mentioned), there is some function h(n) ∈Θ(n2) such that 2n2 g(n) = h(n) for all n. Note that this interpretation implies that 2n2 3n 1 = Θ(n2), which is what the chaining of equations intuitively gives us.
o-notation: The asymptotic upper bound provided by O-notation may or may not be asymptotically tight. The bound 2n2 = O(n2) is asymptotically tight, but the bound 2n = O(n2) is not. We use o-notation to denote an upper bound that is not asymptotically tight. We formally define o(g(n)) ("little-oh of g of n") as the set
o(g(n)) = {f(n) : for any positive constant c > 0, there exists a constant n0 > 0 such that 0 ≤ f(n) < cg(n) for all n ≥ n0}.
For example, 2n = o(n2), but 2n2 ≠ o(n2).
The definitions of O-notation and o-notation are similar. The main difference is that in f(n) = O(g(n)), the bound 0 ≤ f(n) ≤ cg(n) holds for some constant c > 0, but in f(n) = o(g(n)), the bound 0 ≤ f(n) < cg(n) holds for all constants c > 0. Intuitively, in the o-notation, the function f(n) becomes insignificant relative to g(n) as n approaches infinity; that is,
![]()
ω-notation: By analogy, ω-notation is to Ω-notation as o-notation is to O-notation. We use ω-notation to denote a lower bound that is not asymptotically tight. One way to define it is by
f(n) ∈ ω(g(n)) if and only if g(n) ∈ o(f(n)).
Formally, however, we define ω(g(n)) ("little-omega of g of n") as the set
ω(g(n)) = {f(n): for any positive constant c > 0, there exists a constant n0 > 0 such that 0 ≤ cg(n) < f(n) for all n ≥ n0}.
For example, n2/2 = ω(n), but n2/2 ≠ ω(n2). The relation f(n) = ω(g(n)) implies that
![]()
if the limit exists. That is, f(n) becomes arbitrarily large relative to g(n) as n approaches infinity.