Balls And Bins

Balls and bins: Consider the process of randomly tossing identical balls into b bins, numbered 1, 2,..., b. The tosses are independent, and on each toss the ball is equally likely to end up in any bin. The probability that a tossed ball lands in any given bin is 1/b. Thus, the ball-tossing process is a sequence of Bernoulli trials with a probability 1/b of success, where success means that the ball falls in the given bin. This model is particularly useful for analyzing hashing and we can answer a variety of interesting questions about the ball-tossing process.

How many balls fall in a given bin?The number of balls that fall in a given bin follows the binomial distribution b(k; n, 1/b). If n balls are tossed, so the expected number of balls that fall in the given bin is n/b.

How many balls must one toss, on the average, until a given bin contains a ball?The number of tosses until the given bin receives a ball follows the geometric distribution with probability 1/b and, the expected number of tosses until success is 1/(1/b) = b.

How many balls must one toss until every bin contains at least one ball?Let us call a toss in which a ball falls into an empty bin a "hit." We want to know the expected number n of tosses required to get b hits.

The hits can be used to partition the n tosses into stages. The ith stage consists of the tosses after the (i - 1)st hit until the ith hit. The first stage consists of the first toss, since we are guaranteed to have a hit when all bins are empty. For each toss during the ith stage, there are i - 1 bins that contain balls and b - i 1 empty bins. Thus, for each toss in the ith stage, the probability of obtaining a hit is (b-i 1)/b.

Let n_i denote the number of tosses in the ith stage. Thus, the number of tosses required to get b hits is . Each random variable n_i has a geometric distribution with probability of success (b - i 1)/b, and

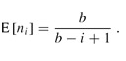
By linearity of expectation,

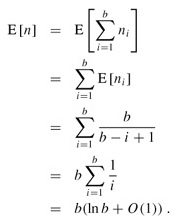
The last line follows from the bound (A.7) on the harmonic series. It therefore takes approximately b ln b tosses before we can expect that every bin has a ball. This problem is also known as the coupon collector's problem, and says that a person trying to collect each of b different coupons must acquire approximately b ln b randomly obtained coupons in order to succeed.