Bounding The Maximum Degree
Bounding the maximum degree: To prove that the amortized time of FIB-HEAP-EXTRACT-MIN and FIB-HEAP-DELETE is O(lg n), we must show that the upper bound D(n) on the degree of any node of an n-node Fibonacci heap is O(lg n). The cuts that occur in FIB-HEAP-DECREASE-KEY, however, may cause trees within the Fibonacci heap to violate the unordered binomial tree properties. In this section, we shall show that because we cut a node from its parent as soon as it loses two children, D(n) is O(lg n). In particular, we shall show that D(n) ≤ ⌊logφn⌋, where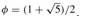 
.
The key to the analysis is as follows. For each node x within a Fibonacci heap, define size(x) to be the number of nodes, including x itself, in the subtree rooted at x. (Note that x need not be in the root list-it can be any node at all.) We shall show that size(x) is exponential in degree[x]. Bear in mind that degree[x] is always maintained as an accurate count of the degree of x.
Let x be any node in a Fibonacci heap, and suppose that degree[x] = k. Let y1, y2, . . . , yk denote the children of x in the order in which they were linked to x, from the earliest to the latest. Then, degree[y1] ≥ 0 and degree[yi] ≥ i - 2 for i = 2, 3, . . . , k.
Proof Obviously, degree[y1] ≥ 0.
For i ≥ 2, we note that when yi was linked to x, all of y1, y2, . . . , yi-1 were children of x, so we must have had degree[x] = i - 1. Node yi is linked to x only if degree[x] = degree[yi], so we must have also had degree[yi] = i - 1 at that time. Since then, node yi has lost at most one child, since it would have been cut from x if it had lost two children. We conclude that degree[yi ] ≥ i - 2.
We finally come to the part of the analysis that explains the name "Fibonacci heaps." Recall from Standard notations and common functions that for k = 0, 1, 2, . . . , the kth Fibonacci number is defined by the recurrence
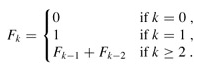
The following lemma gives another way to express Fk.
Lemma 20.2
For all integers k ≥ 0,
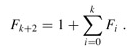
Proof The proof is by induction on k. When k = 0,
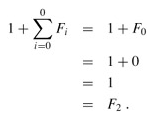
We now assume the inductive hypothesis that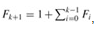 
, and we have
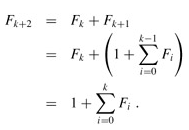
The following lemma and its corollary complete the analysis. They use the in-equality
Fk 2 ≥ φk,