Building A Heap
Building a heap: We can use the procedure MAX-HEAPIFY in a bottom-up manner to convert an array A[1 ‥n], where n = length[A], into a max-heap, the elements in the subarray A[(⌊n/2⌋ 1) ‥n] are all leaves of the tree, and so each is a 1-element heap to begin with. The procedure BUILD-MAX-HEAP goes through the remaining nodes of the tree and runs MAX-HEAPIFY on each one.
BUILD-MAX-HEAP(A)
1 heap-size[A] ← length[A]
2 for i ← ⌊length[A]/2⌋downto 1
3 do MAX-HEAPIFY(A, i)
Figure 6.3shows an example of the action of BUILD-MAX-HEAP.
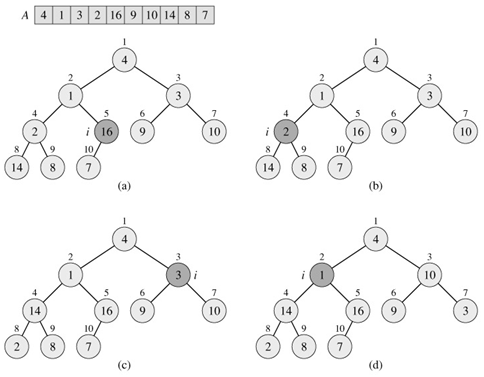
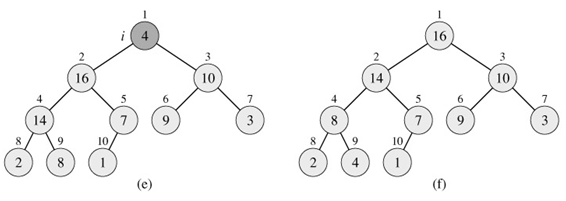
Figure 6.3: The operation of BUILD-MAX-HEAP, showing the data structure before the call to MAX-HEAPIFY in line 3 of BUILD-MAX-HEAP. (a) A 10-element input array A and the binary tree it represents. The figure shows that the loop index i refers to node 5 before the call MAX-HEAPIFY(A, i). (b) The data structure that results. The loop index i for the next iteration refers to node 4. (c)-(e) Subsequent iterations of the for loop in BUILD-MAX-HEAP. Observe that whenever MAX-HEAPIFY is called on a node, the two subtrees of that node are both max-heaps. (f) The max-heap after BUILD-MAX-HEAP finishes.
To show why BUILD-MAX-HEAP works correctly, we use the following loop invariant:
- At the start of each iteration of the for loop of lines 2-3, each node i 1, i 2, . . . , n is the root of a max-heap.
We need to show that this invariant is true prior to the first loop iteration, that each iteration of the loop maintains the invariant, and that the invariant provides a useful property to show correctness when the loop terminates.
- Initialization:Prior to the first iteration of the loop, i = ⌊n/2⌋. Each node ⌊n/2⌋ 1, ⌊n/2⌋ 2, . . . , n is a leaf and is thus the root of a trivial max-heap.
- Maintenance:To see that each iteration maintains the loop invariant, observe that the children of node i are numbered higher than i. By the loop invariant, therefore, they are both roots of max-heaps. This is precisely the condition required for the call MAX-HEAPIFY(A, i) to make node i a max-heap root. Moreover, the MAX-HEAPIFY call preserves the property that nodes i 1, i 2, . . . , n are all roots of max-heaps. Decrementing i in the for loop update reestablishes the loop invariant for the next iteration.
- Termination:At termination, i = 0. By the loop invariant, each node 1, 2, . . . , n is the root of a max-heap. In particular, node 1 is.