Decreasing A Key And Deleting A Node

Figure 20.4: Two calls of FIB-HEAP-DECREASE-KEY. (a) The initial Fibonacci heap. (b) The node with key 46 has its key decreased to 15. The node becomes a root, and its parent (with key 24), which had previously been unmarked, becomes marked. (c)-(e) The node with key 35 has its key decreased to 5. In part (c), the node, now with key 5, becomes a root. Its parent, with key 26, is marked, so a cascading cut occurs. The node with key 26 is cut from its parent and made an unmarked root in (d). Another cascading cut occurs, since the node with key 24 is marked as well. This node is cut from its parent and made an unmarked root in part (e). The cascading cuts stop at this point, since the node with key 7 is a root. (Even if this node were not a root, the cascading cuts would stop, since it is unmarked.) The result of the FIB-HEAP-DECREASE-KEY operation is shown in part (e), with min[H] pointing to the new minimum node.

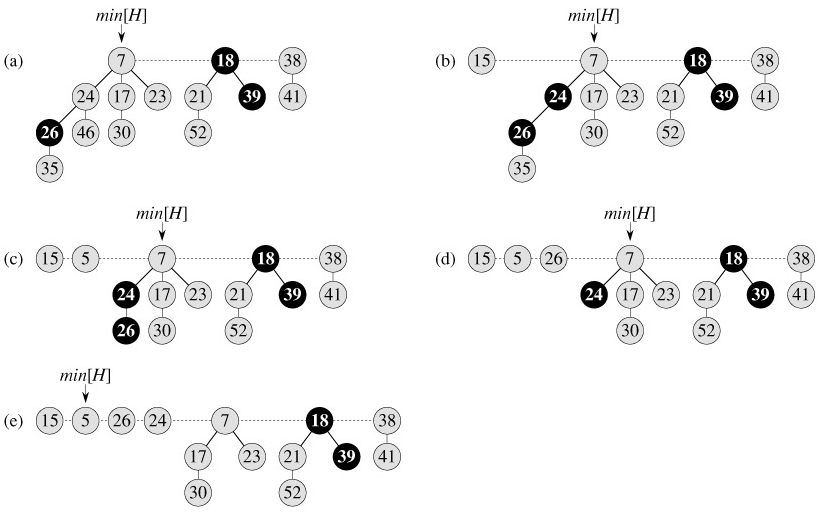
We shall now show that the amortized cost of FIB-HEAP-DECREASE-KEY is only O(1). We start by determining its actual cost. The FIB-HEAP-DECREASE-KEY procedure takes O(1) time, plus the time to perform the cascading cuts. Suppose that CASCADING-CUT is recursively called c times from a given invocation of FIB-HEAP-DECREASE-KEY. Each call of CASCADING-CUT takes O(1) time exclusive of recursive calls. Thus, the actual cost of FIB-HEAP-DECREASE-KEY, including all recursive calls, is O(c).

We next compute the change in potential. Let H denote the Fibonacci heap just prior to the FIB-HEAP-DECREASE-KEY operation. Each recursive call of CASCADING-CUT, except for the last one, cuts a marked node and clears the mark bit. Afterward, there are t(H) c trees (the original t(H) trees, c-1 trees produced by cascading cuts, and the tree rooted at x) and at most m(H) - c 2 marked nodes (c-1 were unmarked by cascading cuts and the last call of CASCADING-CUT may have marked a node). The change in potential is therefore at most

((t(H) c) 2(m(H) - c 2)) - (t(H) 2m(H)) = 4 - c.

Thus, the amortized cost of FIB-HEAP-DECREASE-KEY is at most

O(c) 4 - c = O(1),

since we can scale up the units of potential to dominate the constant hidden in O(c).

You can now see why the potential function was defined to include a term that is twice the number of marked nodes. When a marked node y is cut by a cascading cut, its mark bit is cleared, so the potential is reduced by 2. One unit of potential pays for the cut and the clearing of the mark bit, and the other unit compensates for the unit increase in potential due to node y becoming a root.

Deleting a node

It is easy to delete a node from an n-node Fibonacci heap in O(D(n)) amortized time, as is done by the following pseudocode. We assume that there is no key value of -∞ currently in the Fibonacci heap.

		FIB-HEAP-DELETE(H, x)
1 FIB-HEAP-DECREASE-KEY(H, x, -∞)
2 FIB-HEAP-EXTRACT-MIN(H)

FIB-HEAP-DELETE is analogous to BINOMIAL-HEAP-DELETE. It makes x become the minimum node in the Fibonacci heap by giving it a uniquely small key of -∞. Node x is then removed from the Fibonacci heap by the FIB-HEAP-EXTRACT-MIN procedure. The amortized time of FIB-HEAP-DELETE is the sum of the O(1) amortized time of FIB-HEAP-DECREASE-KEY and the O(D(n)) amortized time of FIB-HEAP-EXTRACT-MIN.