Deleting A Key From A B-tree

Deleting a key from a B-tree: Deletion from a B-tree is analogous to insertion but a little more complicated, because a key may be deleted from any node-not just a leaf-and deletion from an internal node requires that the node's children be rearranged. As in insertion, we must guard against deletion producing a tree whose structure violates the B-tree properties. Just as we had to ensure that a node didn't get too big due to insertion, we must ensure that a node doesn't get too small during deletion (except that the root is allowed to have fewer than the minimum number t - 1 of keys, though it is not allowed to have more than the maximum number 2t - 1 of keys). Just as a simple insertion algorithm might have to back up if a node on the path to where the key was to be inserted was full, a simple approach to deletion might have to back up if a node (other than the root) along the path to where the key is to be deleted has the minimum number of keys.

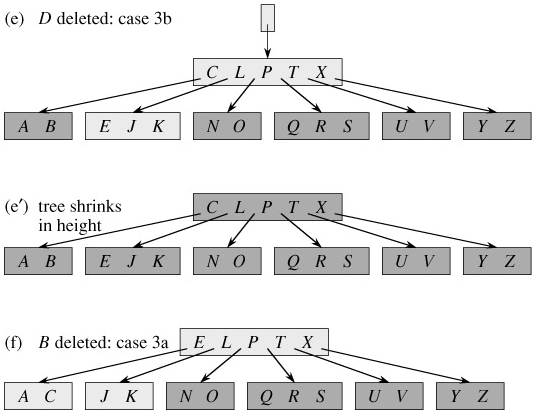
Assume that procedure B-TREE-DELETE is asked to delete the key k from the subtree rooted at x. This procedure is structured to guarantee that whenever B-TREE-DELETE is called recursively on a node x, the number of keys in x is at least the minimum degree t. Note that this condition requires one more key than the minimum required by the usual B-tree conditions, so that sometimes a key may have to be moved into a child node before recursion descends to that child. This strengthened condition allows us to delete a key from the tree in one downward pass without having to "back up" (with one exception, which we'll explain). The following specification for deletion from a B-tree should be interpreted with the understanding that if it ever happens that the root node x becomes an internal node having no keys (this situation can occur in cases 2c and 3b, below), then x is deleted and x's only child c₁[x] becomes the new root of the tree, decreasing the height of the tree by one and preserving the property that the root of the tree contains at least one key (unless the tree is empty).

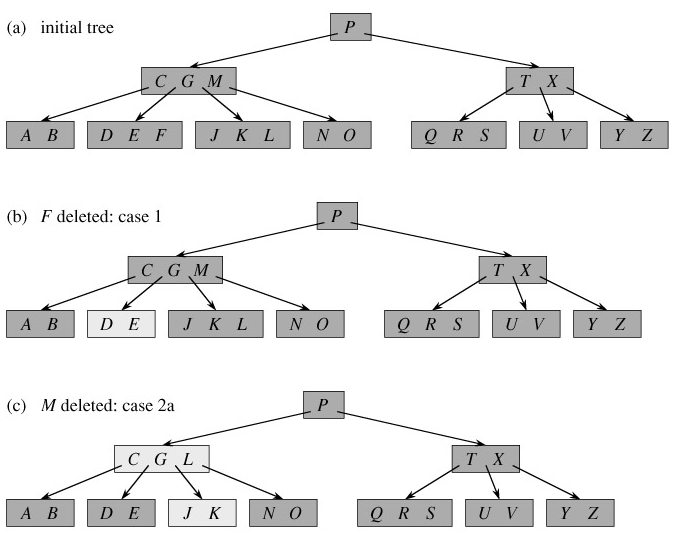
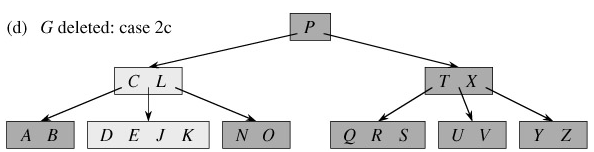
We sketch how deletion works instead of presenting the pseudocode. Figure 18.8 illustrates the various cases of deleting keys from a B-tree.

Figure 18.8: Deleting keys from a B-tree. The minimum degree for this B-tree is t = 3, so a node (other than the root) cannot have fewer than 2 keys. Nodes that are modified are lightly shaded. (a) The B-tree of Figure 18.7(e). (b) Deletion of F. This is case 1: simple deletion from a leaf. (c) Deletion of M. This is case 2a: the predecessor L of M is moved up to take M's position. (d) Deletion of G. This is case 2c: G is pushed down to make node DEGJK, and then G is deleted from this leaf (case 1). (e) Deletion of D. This is case 3b: the recursion can't descend to node CL because it has only 2 keys, so P is pushed down and merged with CL and TX to form CLPTX; then, D is deleted from a leaf (case 1). (e′) After (d), the root is deleted and the tree shrinks in height by one. (f) Deletion of B. This is case 3a: C is moved to fill B's position and E is moved to fill C's position.

If the key k is in node x and x is a leaf, delete the key k from x.
If the key k is in node x and x is an internal node, do the following.
1. If the child y that precedes k in node x has at least t keys, then find the predecessor k′ of k in the subtree rooted at y. Recursively delete k′, and replace k by k′ in x. (Finding k′ and deleting it can be performed in a single downward pass.)
2. Symmetrically, if the child z that follows k in node x has at least t keys, then find the successor k′ of k in the subtree rooted at z. Recursively delete k′, and replace k by k′ in x. (Finding k′ and deleting it can be performed in a single downward pass.)
3. Otherwise, if both y and z have only t - 1 keys, merge k and all of z into y, so that x loses both k and the pointer to z, and y now contains 2t - 1 keys. Then, free z and recursively delete k from y.
If the key k is not present in internal node x, determine the root c_i[x] of the appropriate subtree that must contain k, if k is in the tree at all. If c_i[x] has only t - 1 keys, execute step 3a or 3b as necessary to guarantee that we descend to a node containing at least t keys. Then, finish by recursing on the appropriate child of x.