Determining Whether Any Pair Of Segments Intersects

The sweep-line status is a total order T, for which we require the following operations:

INSERT(T, s): insert segment s into T.
DELETE(T, s): delete segment s from T.
ABOVE(T, s): return the segment immediately above segment s in T.
BELOW(T, s): return the segment immediately below segment s in T.

If there are n segments in the input, we can perform each of the above operations in O(lg n) time using red-black trees. Recall that the red-black-tree operations in Red-Black Trees involve comparing keys. We can replace the key comparisons by comparisons that use cross products to determine the relative ordering of two segments.

Segment-intersection pseudocode: The following algorithm takes as input a set S of n line segments, returning the boolean value TRUE if any pair of segments in S intersects, and FALSE otherwise. The total order T is implemented by a red-black tree.

		ANY-SEGMENTS-INTERSECT(S)
 1  T ← Ø
 2  sort the endpoints of the segments in S from left to right,
             breaking ties by putting left endpoints before right endpoints
             and breaking further ties by putting points with lower
             y-coordinates first
 3  for each point p in the sorted list of endpoints
 4       do if p is the left endpoint of a segment s
 5             then INSERT(T, s)
 6                  if (ABOVE(T, s) exists and intersects s)
                           or (BELOW(T, s) exists and intersects s)
 7                     then return TRUE
 8          if p is the right endpoint of a segment s
 9             then if both ABOVE(T, s) and BELOW(T, s) exist
                            and ABOVE(T, s) intersects BELOW(T, s)
10                     then return TRUE
11                  DELETE(T, s)
12  return FALSE

Figure 33.5 illustrates the execution of the algorithm. Line 1 initializes the total order to be empty. Line 2 determines the event-point schedule by sorting the 2n segment endpoints from left to right, breaking ties as described above. Note that line 2 can be performed by lexicographically sorting the endpoints on (x, e, y), where x and y are the usual coordinates and e = 0 for a left endpoint and e = 1 for a right endpoint.

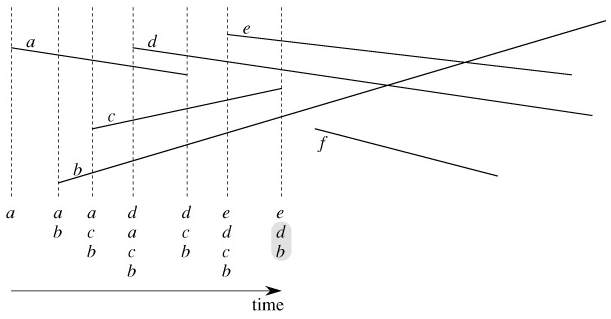
Figure 33.5: The execution of ANY-SEGMENTS-INTERSECT. Each dashed line is the sweep line at an event point, and the ordering of segment names below each sweep line is the total order T at the end of the for loop in which the corresponding event point is processed. The intersection of segments d and b is found when segment c is deleted.

Each iteration of the for loop of lines 3-11 processes one event point p. If p is the left endpoint of a segment s, line 5 adds s to the total order, and lines 6-7 return TRUE if s intersects either of the segments it is consecutive with in the total order defined by the sweep line passing through p. (A boundary condition occurs if p lies on another segment s′. In this case, we require only that s and s′ be placed consecutively into T.) If p is the right endpoint of a segment s, then s is to be deleted from the total order. Lines 9-10 return TRUE if there is an intersection between the segments surrounding s in the total order defined by the sweep line passing through p; these segments will become consecutive in the total order when s is deleted. If these segments do not intersect, line 11 deletes segment s from the total order. Finally, if no intersections are found in processing all the 2n event points, line 12 returns FALSE.

Correctness: To show that ANY-SEGMENTS-INTERSECT is correct, we will prove that the call ANY-SEGMENTS-INTERSECT(S) returns TRUE if and only if there is an intersection among the segments in S.

It is easy to see that ANY-SEGMENTS-INTERSECT returns TRUE (on lines 7 and 10) only if it finds an intersection between two of the input segments. Hence, if it returns TRUE, there is an intersection.

We also need to show the converse: that if there is an intersection, then ANY-SEGMENTS-INTERSECT returns TRUE. Let us suppose that there is at least one intersection. Let p be the leftmost intersection point, breaking ties by choosing the one with the lowest y-coordinate, and let a and b be the segments that intersect at p. Since no intersections occur to the left of p, the order given by T is correct at all points to the left of p. Because no three segments intersect at the same point, there exists a sweep line z at which a and b become consecutive in the total order.^[2] Moreover, z is to the left of p or goes through p. There exists a segment endpoint q on sweep line z that is the event point at which a and b become consecutive in the total order. If p is on sweep line z, then q = p. If p is not on sweep line z, then q is to the left of p. In either case, the order given by T is correct just before q is encountered. (Here is where we use the lexicographic order in which the algorithm processes event points. Because p is the lowest of the leftmost intersection points, even if p is on sweep line z and there is another intersection point p′ on z, event point q = p is processed before the other intersection p′ can interfere with the total order T. Moreover, even if p is the left endpoint of one segment, say a, and the right endpoint of the other segment, say b, because left endpoint events occur before right endpoint events, segment b is in T when segment a is first encountered.) Either event point q is processed by ANY-SEGMENTS-INTERSECT or it is not processed.