Skedbooks
←
Design Analysis of Algorithm

Disjoint-set Forests

Disjoint-set forests: In a faster implementation of disjoint sets, we represent sets by rooted trees, with each node containing one member and each tree representing one set. In a disjoint-set forest, illustrated in Figure 21.4(a), each member points only to its parent. The root of each tree contains the representative and is its own parent. As we shall see, although the straightforward algorithms that use this representation are no faster than ones that use the linked-list representation, by introducing two heuristics-"union by rank" and "path compression"-we can achieve the asymptotically fastest disjoint-set data structure known.

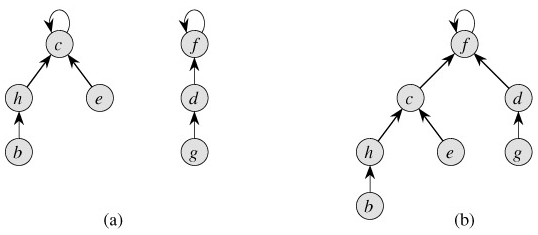
Figure 21.4: A disjoint-set forest. (a) Two trees representing the two sets of Figure 21.2. The tree on the left represents the set {b, c, e, h}, with c as the representative, and the tree on the right represents the set {d, f, g}, with f as the representative. (b) The result of UNION(e, g).

We perform the three disjoint-set operations as follows. A MAKE-SET operation simply creates a tree with just one node. We perform a FIND-SET operation by following parent pointers until we find the root of the tree. The nodes visited on this path toward the root constitute the find path. A UNION operation, shown in Figure 21.4(b), causes the root of one tree to point to the root of the other.

Heuristics to improve the running time

So far, we have not improved on the linked-list implementation. A sequence of n - 1 UNION operations may create a tree that is just a linear chain of n nodes. By using two heuristics, however, we can achieve a running time that is almost linear in the total number of operations m.

The first heuristic, union by rank, is similar to the weighted-union heuristic we used with the linked-list representation. The idea is to make the root of the tree with fewer nodes point to the root of the tree with more nodes. Rather than explicitly keeping track of the size of the subtree rooted at each node, we shall use an approach that eases the analysis. For each node, we maintain a rank that is an upper bound on the height of the node. In union by rank, the root with smaller rank is made to point to the root with larger rank during a UNION operation.

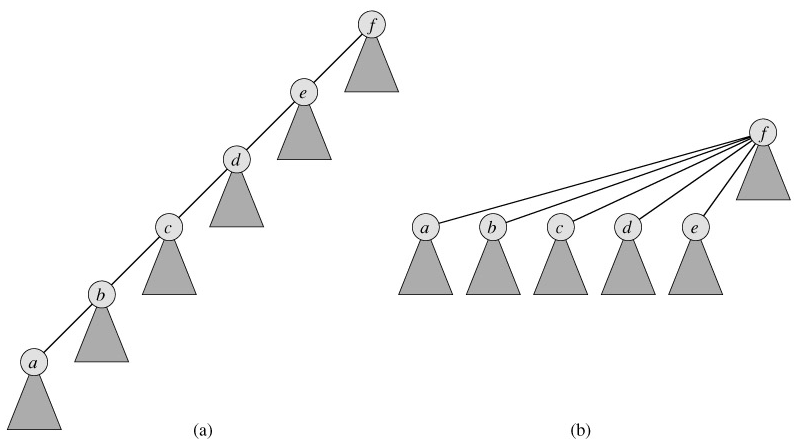
The second heuristic, path compression, is also quite simple and very effective. As shown in Figure 21.5, we use it during FIND-SET operations to make each node on the find path point directly to the root. Path compression does not change any ranks.

Figure 21.5: Path compression during the operation FIND-SET. Arrows and self-loops at roots are omitted. (a) A tree representing a set prior to executing FIND-SET(a). Triangles represent subtrees whose roots are the nodes shown. Each node has a pointer to its parent. (b) The same set after executing FIND-SET(a). Each node on the find path now points directly to the root.

Pseudocode for disjoint-set forests

To implement a disjoint-set forest with the union-by-rank heuristic, we must keep track of ranks. With each node x, we maintain the integer value rank[x], which is an upper bound on the height of x (the number of edges in the longest path between x and a descendant leaf). When a singleton set is created by MAKE-SET, the initial rank of the single node in the corresponding tree is 0. Each FIND-SET operation leaves all ranks unchanged. When applying UNION to two trees, there are two cases, depending on whether the roots have equal rank. If the roots have unequal rank, we make the root of higher rank the parent of the root of lower rank, but the ranks themselves remain unchanged. If, instead, the roots have equal ranks, we arbitrarily choose one of the roots as the parent and increment its rank.

Let us put this method into pseudocode. We designate the parent of node x by p[x]. The LINK procedure, a subroutine called by UNION, takes pointers to two roots as inputs.