Greedy Algorithms

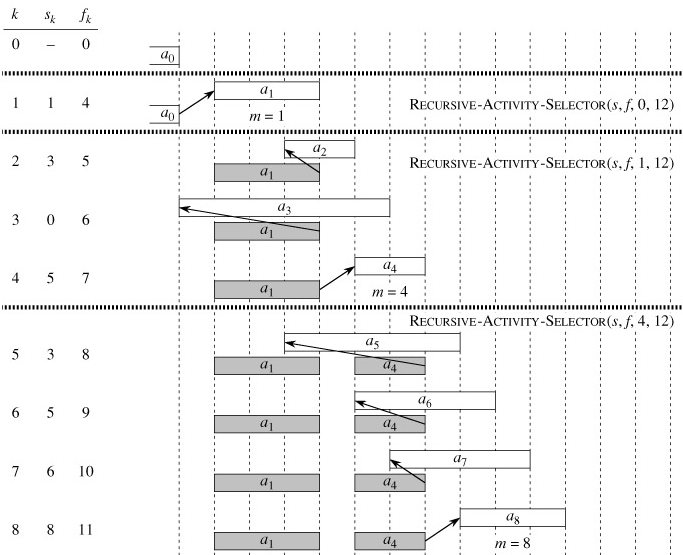
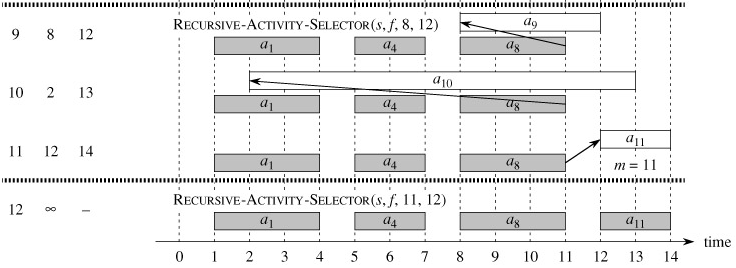
Figure 16.1 shows the operation of the algorithm. In a given recursive call RECURSIVE-ACTIVITY-SELECTOR(s, f, i, j), the while loop of lines 2-3 looks for the first activity in S_ij. The loop examines a_{i 1}, a_{i 2}, ..., a_j-1, until it finds the first activity a_m that is compatible with a_i; such an activity has s_m ≥ f_i. If the loop terminates because it finds such an activity, the procedure returns in line 5 the union of {a_m} and the maximum-size subset of S_mj returned by the recursive call RECURSIVE-ACTIVITY-SELECTOR(s, f, m, j). Alternatively, the loop may terminate because m ≥ j, in which case we have examined all activities whose finish times are before that of a_j without finding one that is compatible with a_i. In this case, S_ij = Ø, and so the procedure returns Ø in line 6.

Figure 16.1: The operation of RECURSIVE-ACTIVITY-SELECTOR on the 11 activities given earlier. Activities considered in each recursive call appear between horizontal lines. The fictitious activity a₀ finishes at time 0, and in the initial call, RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, 12), activity a₁ is selected. In each recursive call, the activities that have already been selected are shaded, and the activity shown in white is being considered. If the starting time of an activity occurs before the finish time of the most recently added activity (the arrow between them points left), it is rejected. Otherwise (the arrow points directly up or to the right), it is selected. The last recursive call, RECURSIVE-ACTIVITY-SELECTOR(s, f, 11, 12), returns Ø. The resulting set of selected activities is {a₁, a₄, a₈, a₁₁}.

Assuming that the activities have already been sorted by finish times, the running time of the call RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n 1) is Θ(n), which we can see as follows. Over all recursive calls, each activity is examined exactly once in the while loop test of line 2. In particular, activity ak is examined in the last call made in which i < k.