Hash Functions

What makes a good hash function?

A good hash function satisfies (approximately) the assumption of simple uniform hashing: each key is equally likely to hash to any of the m slots, independently of where any other key has hashed to. Unfortunately, it is typically not possible to check this condition, since one rarely knows the probability distribution according to which the keys are drawn, and the keys may not be drawn independently.

Occasionally we do know the distribution. For example, if the keys are known to be random real numbers k independently and uniformly distributed in the range 0 ≤ k < 1, the hash function

h(k) = ⌊km⌋

satisfies the condition of simple uniform hashing.

In practice, heuristic techniques can often be used to create a hash function that performs well. Qualitative information about distribution of keys may be useful in this design process. For example, consider a compiler's symbol table, in which the keys are character strings representing identifiers in a program. Closely related symbols, such as pt and pts, often occur in the same program. A good hash function would minimize the chance that such variants hash to the same slot.

A good approach is to derive the hash value in a way that is expected to be independent of any patterns that might exist in the data. For example, the "division method" (discussed in Section 11.3.1) computes the hash value as the remainder when the key is divided by a specified prime number. This method frequently gives good results, assuming that the prime number is chosen to be unrelated to any patterns in the distribution of keys.

Finally, we note that some applications of hash functions might require stronger properties than are provided by simple uniform hashing. For example, we might want keys that are "close" in some sense to yield hash values that are far apart. (This property is especially desirable when we are using linear probing, defined in Section 11.4.) Universal hashing, described in Section 11.3.3, often provides the desired properties.

Interpreting keys as natural numbers

Most hash functions assume that the universe of keys is the set N = {0, 1, 2, ...} of natural numbers. Thus, if the keys are not natural numbers, a way is found to interpret them as natural numbers. For example, a character string can be interpreted as an integer expressed in suitable radix notation. Thus, the identifier pt might be interpreted as the pair of decimal integers (112, 116), since p = 112 and t = 116 in the ASCII character set; then, expressed as a radix-128 integer, pt becomes (112·128) 116 = 14452. It is usually straightforward in an application to devise some such method for interpreting each key as a (possibly large) natural number. In what follows, we assume that the keys are natural numbers.

The division method

In the division method for creating hash functions, we map a key k into one of m slots by taking the remainder of k divided by m. That is, the hash function is

h(k) = k mod m.

For example, if the hash table has size m = 12 and the key is k = 100, then h(k) = 4. Since it requires only a single division operation, hashing by division is quite fast.

When using the division method, we usually avoid certain values of m. For example, m should not be a power of 2, since if m = 2^p, then h(k) is just the p lowest-order bits of k. Unless it is known that all low-order p-bit patterns are equally likely, it is better to make the hash function depend on all the bits of the key. As Exercise 11.3-3 asks you to show, choosing m = 2^p - 1 when k is a character string interpreted in radix 2^p may be a poor choice, because permuting the characters of k does not change its hash value.

A prime not too close to an exact power of 2 is often a good choice for m. For example, suppose we wish to allocate a hash table, with collisions resolved by chaining, to hold roughly n = 2000 character strings, where a character has 8 bits. We don't mind examining an average of 3 elements in an unsuccessful search, so we allocate a hash table of size m = 701. The number 701 is chosen because it is a prime near 2000/3 but not near any power of 2. Treating each key k as an integer, our hash function would be

h(k) = k mod 701.

The multiplication method

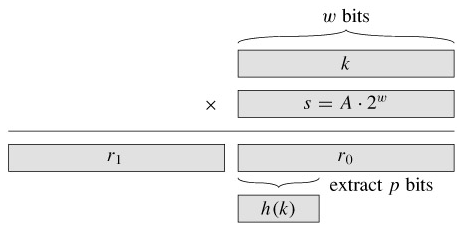
The multiplication method for creating hash functions operates in two steps. First, we multiply the key k by a constant A in the range 0 < A < 1 and extract the fractional part of kA. Then, we multiply this value by m and take the floor of the result. In short, the hash function is

h(k) = ⌊m(kA mod 1)⌋,

where "k A mod 1" means the fractional part of kA, that is, kA - ⌊kA⌋.

An advantage of the multiplication method is that the value of m is not critical. We typically choose it to be a power of 2 (m = 2^p for some integer p) since we can then easily implement the function on most computers as follows. Suppose that the word size of the machine is w bits and that k fits into a single word. We restrict A to be a fraction of the form s/2^w, where s is an integer in the range 0 < s < 2^w. Referring to Figure 11.4, we first multiply k by the w-bit integer s = A · 2^w. The result is a 2w-bit value r₁2^w r₀, where r₁ is the high-order word of the product and r₀ is the low-order word of the product. The desired p-bit hash value consists of the p most significant bits of r₀.