Hash Tables

Hash tables: The difficulty with direct addressing is obvious: if the universe U is large, storing a table T of size |U| may be impractical, or even impossible, given the memory available on a typical computer. Furthermore, the set K of keys actually stored may be so small relative to U that most of the space allocated for T would be wasted.

When the set K of keys stored in a dictionary is much smaller than the universe U of all possible keys, a hash table requires much less storage than a direct-address table. Specifically, the storage requirements can be reduced to Θ(|K|) while we maintain the benefit that searching for an element in the hash table still requires only O(1) time. The only catch is that this bound is for the average time, whereas for direct addressing it holds for the worst-case time.

With direct addressing, an element with key k is stored in slot k. With hashing, this element is stored in slot h(k); that is, we use a hash function h to compute the slot from the key k. Here h maps the universe U of keys into the slots of a hash table T[0 ‥ m - 1]:

h : U → {0, 1, ..., m - 1} .

We say that an element with key k hashes to slot h(k); we also say that h(k) is the hash value of key k. Figure 11.2 illustrates the basic idea. The point of the hash function is to reduce the range of array indices that need to be handled. Instead of |U| values, we need to handle only m values. Storage requirements are correspondingly reduced.

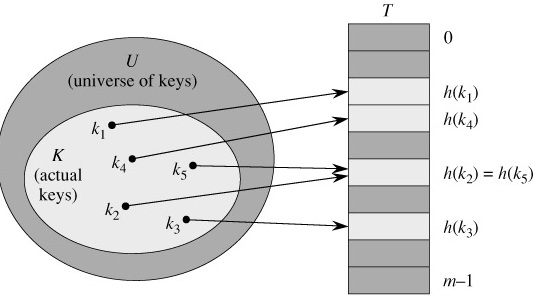
Figure 11.2: Using a hash function h to map keys to hash-table slots. keys k₂ and k₅ map to the same slot, so they collide.

There is one hitch: two keys may hash to the same slot. We call this situation a collision. Fortunately, there are effective techniques for resolving the conflict created by collisions.

Of course, the ideal solution would be to avoid collisions altogether. We might try to achieve this goal by choosing a suitable hash function h. One idea is to make h appear to be "random," thus avoiding collisions or at least minimizing their number. The very term "to hash," evoking images of random mixing and chopping, captures the spirit of this approach. (Of course, a hash function h must be deterministic in that a given input k should always produce the same output h(k).) Since |U| > m, however, there must be at least two keys that have the same hash value; avoiding collisions altogether is therefore impossible. Thus, while a well-designed, "random"-looking hash function can minimize the number of collisions, we still need a method for resolving the collisions that do occur.

The remainder of this section presents the simplest collision resolution technique, called chaining. Section 11.4 introduces an alternative method for resolving collisions, called open addressing.

Collision resolution by chaining: In chaining, we put all the elements that hash to the same slot in a linked list, as shown in Figure 11.3. Slot j contains a pointer to the head of the list of all stored elements that hash to j; if there are no such elements, slot j contains NIL.

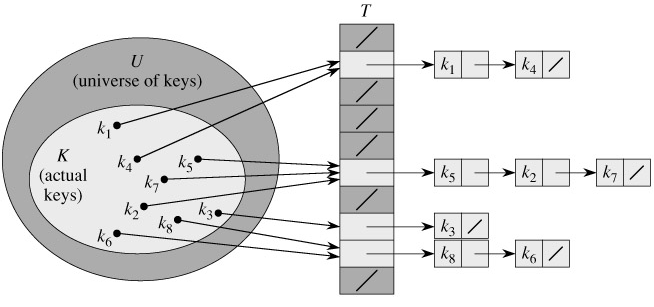
Figure 11.3: Collision resolution by chaining. Each hash-table slot T[j] contains a linked list of all the keys whose hash value is j. For example, h(k₁) = h(k₄) and h(k₅) = h(k₂) = h(k₇).

The dictionary operations on a hash table T are easy to implement when collisions are resolved by chaining.

	CHAINED-HASH-INSERT(T, x)
    insert x at the head of list T[h(key[x])]

CHAINED-HASH-SEARCH(T, k)
    search for an element with key k in list T[h(k)]

CHAINED-HASH-DELETE(T, x)
    delete x from the list T[h(key[x])]

The worst-case running time for insertion is O(1). The insertion procedure is fast in part because it assumes that the element x being inserted is not already present in the table; this assumption can be checked if necessary (at additional cost) by performing a search before insertion. For searching, the worst-case running time is proportional to the length of the list; we shall analyze this operation more closely below. Deletion of an element x can be accomplished in O(1) time if the lists are doubly linked. (Note that CHAINED-HASH-DELETE takes as input an element x and not its key k, so we don't have to search for x first. If the lists were singly linked, it would not be of great help to take as input the element x rather than the key k. We would still have to find x in the list T[h(key[x])], so that the next link of x's predecessor could be properly set to splice x out. In this case, deletion and searching would have essentially the same running time.)