Heaps

Heaps: The (binary) heap data structure is an array object that can be viewed as a nearly complete binary tree as shown in Figure 6.1. Each node of the tree corresponds to an element of the array that stores the value in the node. The tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point. An array A that represents a heap is an object with two attributes: length[A], which is the number of elements in the array, and heap-size[A], the number of elements in the heap stored within array A. That is, although A[1 ‥length[A]] may contain valid numbers, no element past A[heap-size[A]], where heap-size[A] ≤ length[A], is an element of the heap. The root of the tree is A[1], and given the index i of a node, the indices of its parent PARENT(i), left child LEFT(i), and right child RIGHT(i) can be computed simply:

PARENT(i)

   return ⌊i/2⌋

LEFT(i)

   return 2i

RIGHT(i)

   return 2i 1

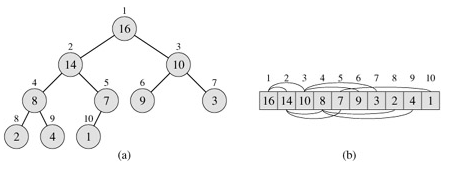
Figure 6.1: A max-heap viewed as (a) a binary tree and (b) an array. The number within the circle at each node in the tree is the value stored at that node. The number above a node is the corresponding index in the array. Above and below the array are lines showing parent-child relationships; parents are always to the left of their children. The tree has height three; the node at index 4 (with value 8) has height one.

On most computers, the LEFT procedure can compute 2i in one instruction by simply shifting the binary representation of i left one bit position. Similarly, the RIGHT procedure can quickly compute 2i 1 by shifting the binary representation of i left one bit position and adding in a 1 as the low-order bit. The PARENT procedure can compute ⌊i/2⌋by shifting i right one bit position. In a good implementation of heapsort, these three procedures are often implemented as "macros" or "in-line" procedures.

There are two kinds of binary heaps: max-heaps and min-heaps. In both kinds, the values in the nodes satisfy a heap property, the specifics of which depend on the kind of heap. In a max-heap, the max-heap property is that for every node i other than the root,

A[PARENT(i)] ≥ A[i] ,

that is, the value of a node is at most the value of its parent. Thus, the largest element in a max-heap is stored at the root, and the subtree rooted at a node contains values no larger than that contained at the node itself. A min-heap is organized in the opposite way; the min-heap property is that for every node i other than the root,

A[PARENT(i)] ≤ A[i] .

The smallest element in a min-heap is at the root.

For the heapsort algorithm, we use max-heaps. Min-heaps are commonly used in priority queues. We shall be precise in specifying whether we need a max-heap or a min-heap for any particular application, and when properties apply to either max-heaps or min-heaps, we just use the term "heap."

Viewing a heap as a tree, we define the height of a node in a heap to be the number of edges on the longest simple downward path from the node to a leaf, and we define the height of the heap to be the height of its root. Since a heap of n elements is based on a complete binary tree, its height is Θ(lg n). We shall see that the basic operations on heaps run in time at most proportional to the height of the tree and thus take O(lg n) time. The remainder of this chapter presents five basic procedures and shows how they are used in a sorting algorithm and a priority-queue data structure.

• The MAX-HEAPIFY procedure, which runs in O(lg n) time, is the key to maintaining the max-heap property.
• The BUILD-MAX-HEAP procedure, which runs in linear time, produces a max-heap from an unordered input array.
• The HEAPSORT procedure, which runs in O(n lg n) time, sorts an array in place.
• The MAX-HEAP-INSERT, HEAP-EXTRACT-MAX, HEAP-INCREASE-KEY, and HEAP-MAXIMUM procedures, which run in O(lg n) time, allow the heap data structure to be used as a priority queue.