Huffman Codes

Constructing a Huffman code

Huffman invented a greedy algorithm that constructs an optimal prefix code called a Huffman code. Keeping in line with our observations in Section 16.2, its proof of correctness relies on the greedy-choice property and optimal substructure. Rather than demonstrating that these properties hold and then developing pseudocode, we present the pseudocode first. Doing so will help clarify how the algorithm makes greedy choices.

In the pseudocode that follows, we assume that C is a set of n characters and that each character c ∈ C is an object with a defined frequency f [c]. The algorithm builds the tree T corresponding to the optimal code in a bottom-up manner. It begins with a set of |C| leaves and performs a sequence of |C| - 1 "merging" operations to create the final tree. A min-priority queue Q, keyed on f , is used to identify the two least-frequent objects to merge together. The result of the merger of two objects is a new object whose frequency is the sum of the frequencies of the two objects that were merged.

	HUFFMAN(C)
1  n ← |C|
2  Q ← C
3  for i 1 to n - 1
4       do allocate a new node z
5          left[z] ← x ← EXTRACT-MIN (Q)
6          right[z] ← y ← EXTRACT-MIN (Q)
7          f [z] ← f [x]   f [y]
8          INSERT(Q, z)
9  return EXTRACT-MIN(Q)   ▹Return the root of the tree.

For our example, Huffman's algorithm proceeds as shown in Figure 16.5. Since there are 6 letters in the alphabet, the initial queue size is n = 6, and 5 merge steps are required to build the tree. The final tree represents the optimal prefix code. The codeword for a letter is the sequence of edge labels on the path from the root to the letter.

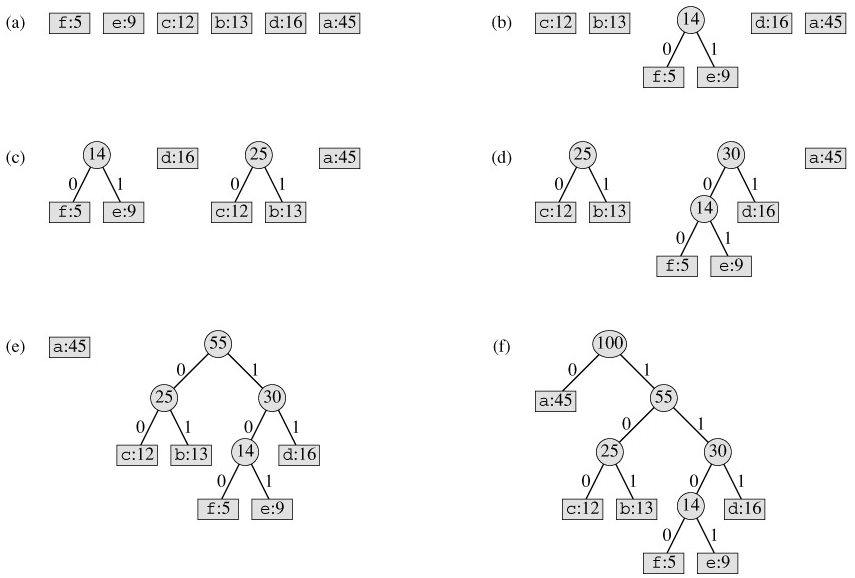
Figure 16.5: The steps of Huffman's algorithm for the frequencies given in Figure 16.3. Each part shows the contents of the queue sorted into increasing order by frequency. At each step, the two trees with lowest frequencies are merged. Leaves are shown as rectangles containing a character and its frequency. Internal nodes are shown as circles containing the sum of the frequencies of its children. An edge connecting an internal node with its children is labeled 0 if it is an edge to a left child and 1 if it is an edge to a right child. The codeword for a letter is the sequence of labels on the edges connecting the root to the leaf for that letter. (a) The initial set of n = 6 nodes, one for each letter. (b)-(e) Intermediate stages. (f) The final tree.

Line 2 initializes the min-priority queue Q with the characters in C. The for loop in lines 3-8 repeatedly extracts the two nodes x and y of lowest frequency from the queue, and replaces them in the queue with a new node z representing their merger. The frequency of z is computed as the sum of the frequencies of x and y in line 7. The node z has x as its left child and y as its right child. (This order is arbitrary; switching the left and right child of any node yields a different code of the same cost.) After n - 1 mergers, the one node left in the queue-the root of the code tree-is returned in line 9.

The analysis of the running time of Huffman's algorithm assumes that Q is implemented as a binary min-heap . For a set C of n characters, the initialization of Q in line 2 can be performed in O (n) time using the BUILD-MIN-HEAP procedure in huffman's algo. The for loop in lines 3-8 is executed exactly n - 1 times, and since each heap operation requires time O (lg n), the loop contributes O (n lg n) to the running time. Thus, the total running time of HUFFMAN on a set of n characters is O (n lg n).