Insertion And Deletion

Insertion and deletion: The operations of insertion and deletion cause the dynamic set represented by a binary search tree to change. The data structure must be modified to reflect this change, but in such a way that the binary-search-tree property continues to hold. As we shall see, modifying the tree to insert a new element is relatively straight-forward, but handling deletion is somewhat more intricate.

Insertion

To insert a new value v into a binary search tree T , we use the procedure TREE-INSERT. The procedure is passed a node z for which key[z] = v, left[z] = NIL, and right[z] = NIL. It modifies T and some of the fields of z in such a way that z is inserted into an appropriate position in the tree.

		TREE-INSERT(T, z)
 1  y ← NIL
 2  x ← root[T]
 3  while x ≠ NIL
 4      do y ←  x
 5         if key[z] < key[x]
 6            then x ← left[x]
 7            else x ← right[x]
 8  p[z] ← y
 9  if y = NIL
10     then root[T] ← z              ⊹ Tree T was empty
11     else if key[z] < key[y]
12             then left[y] ← z
13             else right[y] ← z

Figure 12.3 shows how TREE-INSERT works. Just like the procedures TREE-SEARCH and ITERATIVE-TREE-SEARCH, TREE-INSERT begins at the root of the tree and traces a path downward. The pointer x traces the path, and the pointer y is maintained as the parent of x. After initialization, the while loop in lines 3-7 causes these two pointers to move down the tree, going left or right depending on the comparison of key[z] with key[x], until x is set to NIL. This NIL occupies the position where we wish to place the input item z. Lines 8-13 set the pointers that cause z to be inserted.

Figure 12.3: Inserting an item with key 13 into a binary search tree. Lightly shaded nodes indicate the path from the root down to the position where the item is inserted. The dashed line indicates the link in the tree that is added to insert the item.

Like the other primitive operations on search trees, the procedure TREE-INSERT runs in O(h) time on a tree of height h.

Deletion: The procedure for deleting a given node z from a binary search tree takes as an argument a pointer to z. The procedure considers the three cases shown in Figure 12.4. If z has no children, we modify its parent p[z] to replace z with NIL as its child. If the node has only a single child, we "splice out" z by making a new link between its child and its parent. Finally, if the node has two children, we splice out z's successor y, which has no left child and replace z's key and satellite data with y's key and satellite data.

Figure 12.4: Deleting a node z from a binary search tree. Which node is actually removed depends on how many children z has; this node is shown lightly shaded. (a) If z has no children, we just remove it. (b) If z has only one child, we splice out z. (c) If z has two children, we splice out its successor y, which has at most one child, and then replace z's key and satellite data with y's key and satellite data.

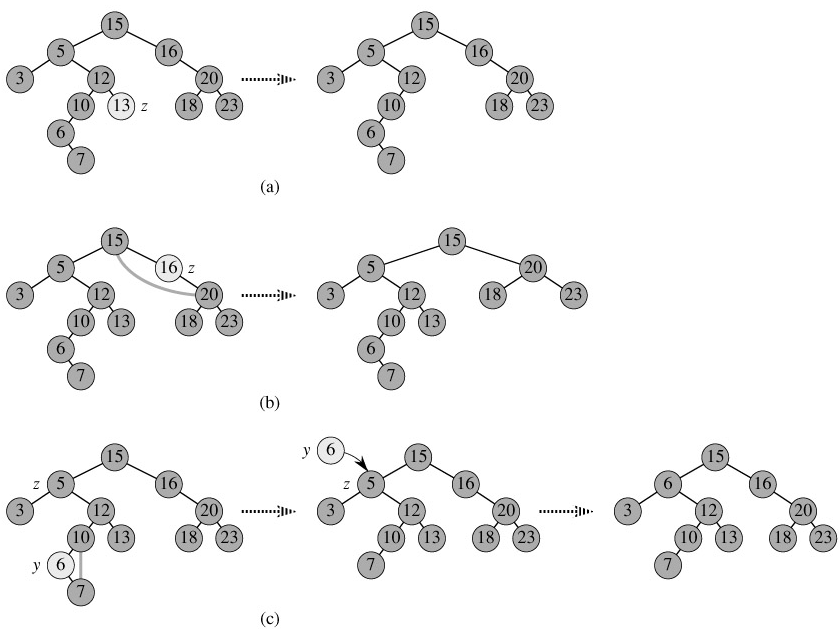
The code for TREE-DELETE organizes these three cases a little differently.

			TREE-DELETE(T, z)
 1  if left[z] = NIL or right[z] = NIL
 2      then y ← z
 3      else y ← TREE-SUCCESSOR(z)
 4  if left[y] ≠ NIL
 5      then x ← left[y]
 6      else x ← right[y]
 7  if x ≠ NIL
 8      then p[x] ← p[y]
 9  if p[y] = NIL
10      then root[T] ← x
11      else if y = left[p[y]]
12              then left[p[y]] ← x
13              else right[p[y]] ← x
14  if y ≠ z
15      then key[z] ← key[y]
16  copy y's satellite data into z
17  return y

In lines 1-3, the algorithm determines a node y to splice out. The node y is either the input node z (if z has at most 1 child) or the successor of z (if z has two children). Then, in lines 4-6, x is set to the non-NIL child of y, or to NIL if y has no children. The node y is spliced out in lines 7-13 by modifying pointers in p[y] and x. Splicing out y is somewhat complicated by the need for proper handling of the boundary conditions, which occur when x = NIL or when y is the root. Finally, in lines 14-16, if the successor of z was the node spliced out, y's key and satellite data are moved to z, overwriting the previous key and satellite data. The node y is returned in line 17 so that the calling procedure can recycle it via the free list. The procedure runs in O(h) time on a tree of height h.