Insertion In Red Black Tree

In cases 2 and 3, the color of z's uncle y is black. The two cases are distinguished by whether z is a right or left child of p[z]. Lines 10-11 constitute case 2, which is shown in Figure 13.6 together with case 3. In case 2, node z is a right child of its parent. We immediately use a left rotation to transform the situation into case 3 (lines 12-14), in which node z is a left child. Because both z and p[z] are red, the rotation affects neither the black-height of nodes nor property 5. Whether we enter case 3 directly or through case 2, z's uncle y is black, since otherwise we would have executed case 1. Additionally, the node p[p[z]] exists, since we have argued that this node existed at the time that lines 2 and 3 were executed, and after moving z up one level in line 10 and then down one level in line 11, the identity of p[p[z]] remains unchanged. In case 3, we execute some color changes and a right rotation, which preserve property 5, and then, since we no longer have two red nodes in a row, we are done. The body of the while loop is not executed another time, since p[z] is now black.

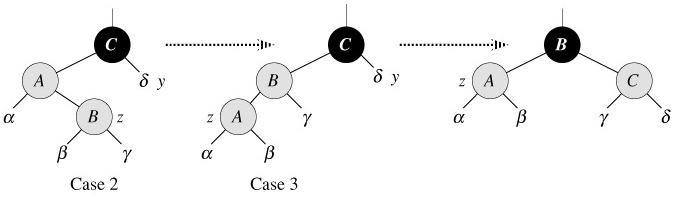
Figure 13.6: Cases 2 and 3 of the procedure RB-INSERT. As in case 1, property 4 is violated in either case 2 or case 3 because z and its parent p[z] are both red. Each of the subtrees α, β, γ, and δ has a black root (α, β, and γ from property 4, and δ because otherwise we would be in case 1), and each has the same black-height. Case 2 is transformed into case 3 by a left rotation, which preserves property 5: all downward paths from a node to a leaf have the same number of blacks. Case 3 causes some color changes and a right rotation, which also preserve property 5. The while loop then terminates, because property 4 is satisfied: there are no longer two red nodes in a row.

Now we show that cases 2 and 3 maintain the loop invariant. (As we have just argued, p[z] will be black upon the next test in line 1, and the loop body will not execute again.)

Case 2 makes z point to p[z], which is red. No further change to z or its color occurs in cases 2 and 3.
Case 3 makes p[z] black, so that if p[z] is the root at the start of the next iteration, it is black.
As in case 1, properties 1, 3, and 5 are maintained in cases 2 and 3.

Since node z is not the root in cases 2 and 3, we know that there is no violation of property 2. Cases 2 and 3 do not introduce a violation of property 2, since the only node that is made red becomes a child of a black node by the rotation in case 3.

Cases 2 and 3 correct the lone violation of property 4, and they do not intro- duce another violation.

Having shown that each iteration of the loop maintains the invariant, we have shown that RB-INSERT-FIXUP correctly restores the red-black properties.

Analysis

What is the running time of RB-INSERT? Since the height of a red-black tree on n nodes is O(lg n), lines 1-16 of RB-INSERT take O(lg n) time. In RB-INSERT- FIXUP, the while loop repeats only if case 1 is executed, and then the pointer z moves two levels up the tree. The total number of times the while loop can be executed is therefore O(lg n). Thus, RB-INSERT takes a total of O(lg n) time. Interestingly, it never performs more than two rotations, since the while loop terminates if case 2 or case 3 is executed.