Interval Trees

Before we see why INTERVAL-SEARCH is correct, let's examine how it works on the interval tree in Figure 14.4. Suppose we wish to find an interval that overlaps the interval i = [22, 25]. We begin with x as the root, which contains [16, 21] and does not overlap i. Since max[left[x]] = 23 is greater than low[i] = 22, the loop continues with x as the left child of the root-the node containing [8, 9], which also does not overlap i. This time, max[left[x]] = 10 is less than low[i] = 22, so the loop continues with the right child of x as the new x. The interval [15, 23] stored in this node overlaps i, so the procedure returns this node.

As an example of an unsuccessful search, suppose we wish to find an interval that overlaps i = [11, 14] in the interval tree of Figure 14.4. We once again begin with x as the root. Since the root's interval [16, 21] does not overlap i, and since max[left[x]] = 23 is greater than low[i] = 11, we go left to the node containing [8, 9]. (Note that no interval in the right subtree overlaps i-we shall see why later.) Interval [8, 9] does not overlap i, and max[left[x]] = 10 is less than low[i] = 11, so we go right. (Note that no interval in the left subtree overlaps i.) Interval [15, 23] does not overlap i, and its left child is nil[T], so we go right, the loop terminates, and the sentinel nil[T] is returned.

Theorem 14.2: Any execution of INTERVAL-SEARCH(T, i) either returns a node whose interval overlaps i, or it returns nil[T] and the tree T contains no node whose interval overlaps i.

Proof: The while loop of lines 2-5 terminates either when x = nil[T] or i overlaps int[x]. In the latter case, it is certainly correct to return x. Therefore, we focus on the former case, in which the while loop terminates because x = nil[T].

We use the following invariant for the while loop of lines 2-5:

If tree T contains an interval that overlaps i, then there is such an interval in the subtree rooted at x.

We use this loop invariant as follows:

Initialization: Prior to the first iteration, line 1 sets x to be the root of T , so that the invariant holds.

Maintenance: In each iteration of the while loop, either line 4 or line 5 is executed. We shall show that the loop invariant is maintained in either case.

If line 5 is executed, then because of the branch condition in line 3, we have left[x] = nil[T], or max[left[x]]< low[i]. If left[x] = nil[T], the subtree rooted at left[x] clearly contains no interval that overlaps i, and so setting x to right[x] maintains the invariant. Suppose, therefore, that left[x] ≠ nil[T] and max[left[x]]< low[i]. As Figure 14.5(a) shows, for each interval i' in x's left subtree, we have

high[i']	≤	max[left[x]]
	<	low[i].

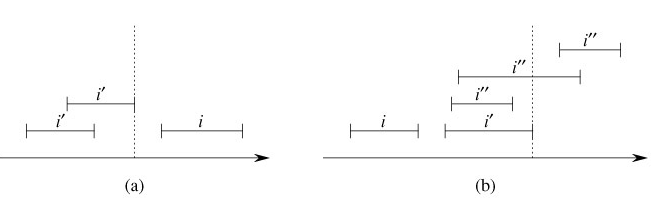
Figure 14.5: Intervals in the proof of Theorem 14.2. The value of max[left[x]] is shown in each case as a dashed line. (a) The search goes right. No interval i' in x's left subtree can overlap i. (b) The search goes left. The left subtree of x contains an interval that overlaps i (situation not shown), or there is an interval i' in x's left subtree such that high[i'] = max[left[x]]. Since i does not overlap i', neither does it overlap any interval i" in x's right subtree, since low[i'] ≤ low[i"].

By the interval trichotomy, therefore, i' and i do not overlap. Thus, the left subtree of x contains no intervals that overlap i, so that setting x to right[x] maintains the invariant.

If, on the other hand, line 4 is executed, then we will show that the contrapositive of the loop invariant holds. That is, if there is no interval overlapping i in the subtree rooted at left[x], then there is no interval overlapping i anywhere in the tree. Since line 4 is executed, then because of the branch condition in line 3, we have max[left[x]] ≥ low[i]. Moreover, by definition of the max field, there must be some interval i' in x's left subtree such that

high[i']	=	max[left[x]]
	≥	low[i].

(Figure 14.5(b) illustrates the situation.) Since i and i' do not overlap, and since it is not true that high[i']< low[i], it follows by the interval trichotomy that high[i]< low[i']. Interval trees are keyed on the low endpoints of intervals, and thus the search-tree property implies that for any interval i" in x's right subtree,

high[i]	<	low[i']
	≤	low[i"].

By the interval trichotomy, i and i" do not overlap. We conclude that whether or not any interval in x's left subtree overlaps i, setting x to left[x] maintains the invariant.

Termination: If the loop terminates when x = nil[T], there is no interval overlapping i in the subtree rooted at x. The contrapositive of the loop invariant implies that T contains no interval that overlaps i. Hence it is correct to return x = nil[T].