Inverting Matrices

Inverting matrices

Although in practice we do not generally use matrix inverses to solve systems of linear equations, preferring instead to use more numerically stable techniques such as LUP decomposition, it is sometimes necessary to compute a matrix inverse. In this section, we show how LUP decomposition can be used to compute a matrix inverse. We also prove that matrix multiplication and computing the inverse of a matrix are equivalently hard problems, in that (subject to technical conditions) we can use an algorithm for one to solve the other in the same asymptotic running time. Thus, we can use Strassen's algorithm for matrix multiplication to invert a matrix. Indeed, Strassen's original paper was motivated by the problem of showing that a set of a linear equations could be solved more quickly than by the usual method.

Computing a matrix inverse from an LUP decomposition

Suppose that we have an LUP decomposition of a matrix A in the form of three matrices L, U , and P such that PA = LU. Using LUP-SOLVE, we can solve an equation of the form Ax = b in time Θ(n²). Since the LUP decomposition depends on A but not b, we can run LUP-SOLVE on a second set of equations of the form Ax = b' in additional time Θ(n²). In general, once we have the LUP decomposition of A, we can solve, in time Θ(kn²), k versions of the equation Ax = b that differ only in b.

The equation

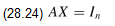
can be viewed as a set of n distinct equations of the form Ax = b. These equations define the matrix X as the inverse of A. To be precise, let X_i denote the ith column of X, and recall that the unit vector e_i is the ith column of I_n. Equation (28.24) can then be solved for X by using the LUP decomposition for A to solve each equation

AX_i = e_i

separately for X_i. Each of the n columns X_i can be found in time Θ(n²), and so the computation of X from the LUP decomposition of A takes time Θ(n³). Since the LUP decomposition of A can be computed in time Θ(n³), the inverse A^-1 of a matrix A can be determined in time Θ(n³).

Matrix multiplication and matrix inversion

We now show that the theoretical speedups obtained for matrix multiplication translate to speedups for matrix inversion. In fact, we prove something stronger: matrix inversion is equivalent to matrix multiplication, in the following sense. If M(n) denotes the time to multiply two n × n matrices, then there is a way to invert an n × n matrix in time O (M(n)). Moreover, if I (n) denotes the time to invert a nonsingular n × n matrix, then there is a way to multiply two n × n matrices in time O (I(n)). We prove these results as two separate theorems.