Johnson's Algorithm For Sparse Graphs

Johnson's algorithm for sparse graphs: Johnson's algorithm finds shortest paths between all pairs in O(V² lg V V E) time. For sparse graphs, it is asymptotically better than either repeated squaring of matrices or the Floyd-Warshall algorithm. The algorithm either returns a matrix of shortest-path weights for all pairs of vertices or reports that the input graph contains a negative-weight cycle. Johnson's algorithm uses as subroutines both Dijkstra's algorithm and the Bellman-Ford algorithm, which are described in Single-Source Shortest Paths.

Johnson's algorithm uses the technique of reweighting, which works as follows. If all edge weights w in a graph G = (V, E) are nonnegative, we can find shortest paths between all pairs of vertices by running Dijkstra's algorithm once from each vertex; with the Fibonacci-heap min-priority queue, the running time of this all-pairs algorithm is O(V² lg V V E). If G has negative-weight edges but no negative-weight cycles, we simply compute a new set of nonnegative edge weights that allows us to use the same method. The new set of edge weights  must satisfy two important properties.

1. For all pairs of vertices u, v ∈ V, a path p is a shortest path from u to v using weight function w if and only if p is also a shortest path from u to v using weight function .

2. For all edges (u, v), the new weight is nonnegative.

As we shall see in a moment, the preprocessing of G to determine the new weight function can be performed in O(V E) time.

Preserving shortest paths by reweighting

As the following lemma shows, it is easy to come up with a reweighting of the edges that satisfies the first property above. We use δ to denote shortest-path weights derived from weight function w and to denote shortest-path weights derived from weight function .

Producing nonnegative weights by reweighting

Our next goal is to ensure that the second property holds: we want to be nonnegative for all edges (u, v) ∈ E. Given a weighted, directed graph G = (V, E) with weight function w : E → R, we make a new graph G′ = (V′, E′), where V′ = V ∪ {s} for some new vertex s ∉ V and E′ = E ∪ {(s, v) : v ∈ V}. We extend the weight function w so that w(s, v) = 0 for all v ∈ V . Note that because s has no edges that enter it, no shortest paths in G′, other than those with source s, contain s. Moreover, G′ has no negative-weight cycles if and only if G has no negative-weight cycles. Figure 25.6(a) shows the graph G′ corresponding to the graph G of Figure 25.1.

 

 

 

 

 

 

 

 

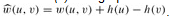Figure 25.6: Johnson's all-pairs shortest-paths algorithm run of the graph of Figure 25.1. (a) The graph G′ with the original weight function w. The new vertex s is black. Within each vertex v is h(v) = δ(s, v). (b) Each edge (u, v) is reweighted with weight function . (c)-(g) The result of running Dijkstra's algorithm on each vertex of G using weight function 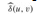. In each part, the source vertex u is black, and shaded edges are in the shortest-paths tree computed by the algorithm. Within each vertex v are the values 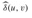and δ(u, v), separated by a slash. The value d_uv = δ(u, v) is equal to .

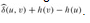Now suppose that G and G′ have no negative-weight cycles. Let us define h(v) = δ(s, v) for all v ∈ V′. By the triangle inequality, we have h(v) ≤ h(u) w(u, v) for all edges (u, v) ∈ E′. Thus, if we define the new weights according to equation (25.9), we have , and the second property is satisfied. Figure 25.6(b) shows the graph G′ from Figure 25.6(a) with reweighted edges.