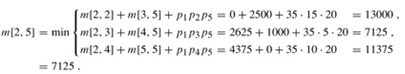Matrix-chain Multiplication

	MATRIX-CHAIN-ORDER(p)
 1 n ← length[p] - 1
 2 for i ← 1 to n
 3      do m[i, i] ← 0
 4 for l ← 2 to n      ▹l is the chain length.
 5      do for i ← 1 to n - l   1
 6             do j ← i   l - 1
 7                m[i, j] ← ∞
 8                for k ← i to j - 1
 9                    do q ← m[i, k]   m[k   1, j]   pi-1 pkpj
10                       if q < m[i, j]
11                          then m[i, j] ← q
12                               s[i, j] ← k
13 return m and s

The algorithm first computes m[i, i] ← 0 for i = 1, 2, ..., n (the minimum costs for chains of length 1) in lines 2-3. It then uses recurrence (15.12) to compute m[i, i 1] for i = 1, 2, ..., n - 1 (the minimum costs for chains of length l = 2) during the first execution of the loop in lines 4-12. The second time through the loop, it computes m[i, i 2] for i = 1, 2, ..., n - 2 (the minimum costs for chains of length l = 3), and so forth. At each step, the m[i, j] cost computed in lines 9-12 depends only on table entries m[i, k] and m[k 1, j] already computed.

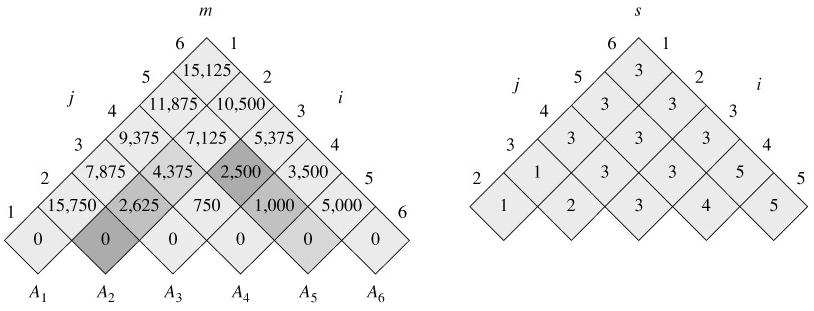
Figure 15.3 illustrates this procedure on a chain of n = 6 matrices. Since we have defined m[i, j] only for i ≤ j, only the portion of the table m strictly above the main diagonal is used. The figure shows the table rotated to make the main diagonal run horizontally. The matrix chain is listed along the bottom. Using this layout, the minimum cost m[i, j] for multiplying a subchain A_i A_{i 1} A_j of matrices can be found at the intersection of lines running northeast from A_i and northwest from A_j. Each horizontal row in the table contains the entries for matrix chains of the same length. MATRIX-CHAIN-ORDER computes the rows from bottom to top and from left to right within each row. An entry m[i, j] is computed using the products p_i-1 p_k p_j for k = i, i 1, ..., j - 1 and all entries southwest and southeast from m[i, j].

The tables are rotated so that the main diagonal runs horizontally. Only the main diagonal and upper triangle are used in the m table, and only the upper triangle is used in the s table. The minimum number of scalar multiplications to multiply the 6 matrices is m[1, 6] = 15,125. Of the darker entries, the pairs that have the same shading are taken together in line 9 when computing