Maximum Bipartite Matching

Maximum bipartite matching: Some combinatorial problems can easily be cast as maximum-flow problems. The multiple-source, multiple-sink maximum-flow problem from Section 26.1 gave us one example. There are other combinatorial problems that seem on the surface to have little to do with flow networks, but can in fact be reduced to maximum-flow problems. This section presents one such problem: finding a maximum matching in a bipartite graph (see Section B.4). In order to solve this problem, we shall take advantage of an integrality property provided by the Ford-Fulkerson method. We shall also see that the Ford-Fulkerson method can be made to solve the maximum-bipartite-matching problem on a graph G = (V, E) in O(V E) time.

The maximum-bipartite-matching problem

Given an undirected graph G = (V, E), a matching is a subset of edges M ⊆ E such that for all vertices v ∈ V, at most one edge of M is incident on v. We say that a vertex v ∈ V is matched by matching M if some edge in M is incident on v; otherwise, v is unmatched. A maximum matching is a matching of maximum cardinality, that is, a matching M such that for any matching M', we have |M| ≥ |M'|. In this section, we shall restrict our attention to finding maximum matchings in bipartite graphs. We assume that the vertex set can be partitioned into V = L ∪ R, where L and R are disjoint and all edges in E go between L and R. We further assume that every vertex in V has at least one incident edge. Figure 26.7 illustrates the notion of a matching.

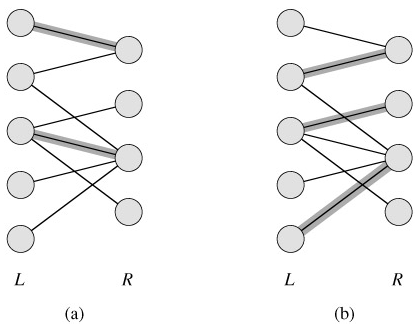
Figure 26.7: A bibartite graph G = (V, E) with vertex partition V = L∪R. (a) A matching with cardinality 2. (b) A maximum matching with cardinality 3.

The problem of finding a maximum matching in a bipartite graph has many practical applications. As an example, we might consider matching a set L of machines with a set R of tasks to be performed simultaneously. We take the presence of edge (u, v) in E to mean that a particular machine u ∈ L is capable of performing a particular task v ∈ R. A maximum matching provides work for as many machines as possible.

Finding a maximum bipartite matching

We can use the Ford-Fulkerson method to find a maximum matching in an undirected bipartite graph G = (V, E) in time polynomial in |V| and |E|. The trick is to construct a flow network in which flows correspond to matchings, as shown in Figure 26.8. We define the corresponding flow network G' = (V', E') for the bipartite graph G as follows. We let the source s and sink t be new vertices not in V, and we let V' = V ∪ {s, t}. If the vertex partition of G is V = L ∪ R, the directed edges of G' are the edges of E, directed from L to R, along with V new edges:

{(s, u) : u ∈ L}

∪{(u, v) : u ∈ L, v ∈ R, and (u, v) ∈ E}

∪{(v, t) : v ∈ R}.

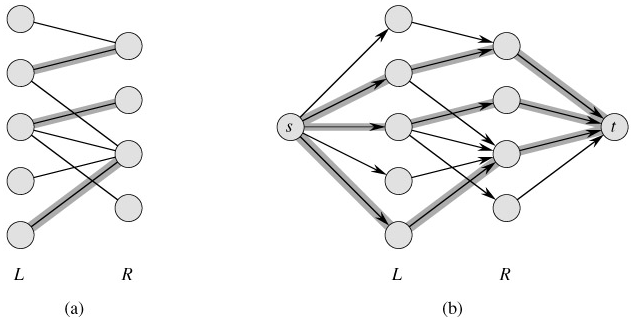
Figure 26.8: The flow network corresponding to a bipartite graph. (a) The bipartite graph G = (V, E) with vertex partition V = L ∪ R from Figure 26.7. A maximum matching is shown by shaded edges. (b) The corresponding flow network G' with a maximum flow shown. Each edge has unit capacity. Shaded edges have a flow of 1, and all other edges carry no flow. The shaded edges from L to R correspond to those in a maximum matching of the bipartite graph.

To complete the construction, we assign unit capacity to each edge in E'. Since each vertex in V has at least one incident edge, |E| ≥ |V|/2. Thus, |E| ≤ |E'| = |E| |V| ≤ 3|E|, and so |E'| = Θ(E).

The following lemma shows that a matching in G corresponds directly to a flow in G's corresponding flow network G'. We say that a flow f on a flow network G = (V, E) is integer-valued if f (u, v) is an integer for all (u, v) ∈ V × V.