Np-completeness Proofs
NP-completeness proofs: The NP-completeness of the circuit-satisfiability problem relies on a direct proof that L ≤P CIRCUIT-SAT for every language L ∈ NP. In this section, we shall show how to prove that languages are NP-complete without directly reducing every language in NP to the given language. We shall illustrate this methodology by proving that various formula-satisfiability problems are NP-complete. NP-complete problems provides many more examples of the methodology. In other words, by reducing a known NP-complete language L′ to L, we implicitly reduce every language in NP to L. Thus,
-
Prove L ∈ NP.
-
Select a known NP-complete language L′.
-
Describe an algorithm that computes a function f mapping every instance x ∈ {0, 1}* of L′ to an instance f(x) of L.
-
Prove that the function f satisfies x ∈ L′ if and only if f (x) ∈ L for all x ∈ {0, 1}*.
-
Prove that the algorithm computing f runs in polynomial time.
(Steps 2-5 show that L is NP-hard.) This methodology of reducing from a single known NP-complete language is far simpler than the more complicated process of showing directly how to reduce from every language in NP. Proving CIRCUIT-SAT ∈ NPC has given us a "foot in the door." Knowing that the circuit-satisfiability problem is NP-complete now allows us to prove much more easily that other problems are NP-complete. Moreover, as we develop a catalog of known NP-complete problems, we will have more and more choices for languages from which to reduce.
Formula satisfiability: We illustrate the reduction methodology by giving an NP-completeness proof for the problem of determining whether a boolean formula, not a circuit, is satisfiable. This problem has the historical honor of being the first problem ever shown to be NP-complete.
We formulate the (formula) satisfiability problem in terms of the language SAT as follows. An instance of SAT is a boolean formula φ composed of
-
n boolean variables: x1, x2, ..., xn;
-
m boolean connectives: any boolean function with one or two inputs and one output, such as ∨ (AND), ∧ (OR), ¬ (NOT), → (implication), ↔ (if and only if); and
-
parentheses. (Without loss of generality, we assume that there are no redundant parentheses, i.e., there is at most one pair of parentheses per boolean connective.)
It is easy to encode a boolean formula φ in a length that is polynomial in n m. As in boolean combinational circuits, a truth assignment for a boolean formula φ is a set of values for the variables of φ, and a satisfying assignment is a truth assignment that causes it to evaluate to 1. A formula with a satisfying assignment is a satisfiable formula. The satisfiability problem asks whether a given boolean formula is satisfiable; in formal-language terms,
SAT = {〈φ〉 : φ is a satisfiable boolean formula}.
As an example, the formula
φ = ((x1 → x2) ∧ ¬((¬x1 ↔ x3) ∨ x4)) ∨ ¬x2
has the satisfying assignment 〈x1 = 0, x2 = 0, x3 = 1, x4 = 1〉, since
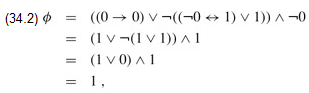
and thus this formula φ belongs to SAT.
The naive algorithm to determine whether an arbitrary boolean formula is satisfiable does not run in polynomial time. There are 2n possible assignments in a formula φ with n variables. If the length of 〈φ〉 is polynomial in n, then checking every assignment requires Ω(2n) time, which is superpolynomial in the length of 〈φ〉. As the following theorem shows, a polynomial-time algorithm is unlikely to exist.
3-CNF satisfiability: Many problems can be proved NP-complete by reduction from formula satisfiability. The reduction algorithm must handle any input formula, though, and this requirement can lead to a huge number of cases that must be considered. It is often desirable, therefore, to reduce from a restricted language of boolean formulas, so that fewer cases need be considered. Of course, we must not restrict the language so much that it becomes polynomial-time solvable. One convenient language is 3-CNF satisfiability, or 3-CNF-SAT.
We define 3-CNF satisfiability using the following terms. A literal in a boolean formula is an occurrence of a variable or its negation. A boolean formula is in conjunctive normal form, or CNF, if it is expressed as an AND of clauses, each of which is the OR of one or more literals. A boolean formula is in 3-conjunctive normal form, or 3-CNF, if each clause has exactly three distinct literals.
For example, the boolean formula
(x1 ∨ ¬x1 ∨ ¬x2) ∧ (x3 ∨ x2 ∨ x4) ∧ (¬x1 ∨ ¬x3 ∨ ¬x4)
is in 3-CNF. The first of its three clauses is (x1 ∨ ¬x1 ∨ ¬x2), which contains the three literals x1, ¬x1, and ¬x2.
In 3-CNF-SAT, we are asked whether a given boolean formula φ in 3-CNF is satisfiable. The following theorem shows that a polynomial-time algorithm that can determine the satisfiability of boolean formulas is unlikely to exist, even when they are expressed in this simple normal form.