Perfect Hashing

Perfect hashing: Although hashing is most often used for its excellent expected performance, hashing can be used to obtain excellent worst-case performance when the set of keys is static: once the keys are stored in the table, the set of keys never changes. Some applications naturally have static sets of keys: consider the set of reserved words in a programming language, or the set of file names on a CD-ROM. We call a hashing technique perfect hashing if the worst-case number of memory accesses required to perform a search is O(1).

The basic idea to create a perfect hashing scheme is simple. We use a two-level hashing scheme with universal hashing at each level. Figure 11.6 illustrates the approach.

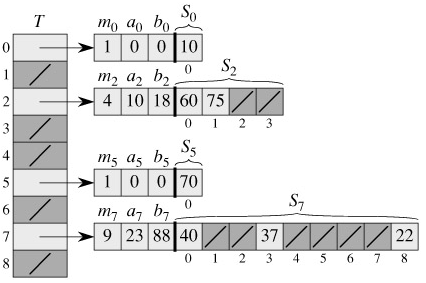
Figure 11.6: Using perfect hashing to store the set K = {10, 22, 37, 40, 60, 70, 75}. The outer hash function is h(k) = ((ak b) mod p) mod m, where a = 3, b = 42, p = 101, and m = 9. For example, h(75) = 2, so key 75 hashes to slot 2 of table T . A secondary hash table S_j stores all keys hashing to slot j . The size of hash table S_j is m_j , and the associated hash function is h_j (k) = ((a_j k b_j) mod p) mod m_j. Since h₂(75) = 1, key 75 is stored in slot 1 of secondary hash table S₂. There are no collisions in any of the secondary hash tables, and so searching takes constant time in the worst case.

The first level is essentially the same as for hashing with chaining: the n keys are hashed into m slots using a hash function h carefully selected from a family of universal hash functions.

Instead of making a list of the keys hashing to slot j, however, we use a small secondary hash table S_j with an associated hash function h_j. By choosing the hash functions h_j carefully, we can guarantee that there are no collisions at the secondary level.

In order to guarantee that there are no collisions at the secondary level, however, we will need to let the size m_j of hash table S_j be the square of the number n_j of keys hashing to slot j. While having such a quadratic dependence of m_j on n_j may seem likely to cause the overall storage requirements to be excessive, we shall show that by choosing the first level hash function well, the expected total amount of space used is still O(n).

We shall proceed in two steps. First, we shall determine how to ensure that the secondary tables have no collisions. Second, we shall show that the expected amount of memory used overall-for the primary hash table and all the secondary hash tables-is O(n).