Performance Of Quicksort

Performance of quicksort: The running time of quicksort depends on whether the partitioning is balanced or unbalanced, and this in turn depends on which elements are used for partitioning. If the partitioning is balanced, the algorithm runs asymptotically as fast as merge sort. If the partitioning is unbalanced, however, it can run asymptotically as slowly as insertion sort. In this section, we shall informally investigate how quicksort performs under the assumptions of balanced versus unbalanced partitioning.

Worst-case partitioning: The worst-case behavior for quicksort occurs when the partitioning routine produces one subproblem with n - 1 elements and one with 0 elements. Let us assume that this unbalanced partitioning arises in each recursive call. The partitioning costs Θ(n) time. Since the recursive call on an array of size 0 just returns, T(0) = Θ(1), and the recurrence for the running time is

Intuitively, if we sum the costs incurred at each level of the recursion, we get an arithmetic series (equation (A.2)), which evaluates to Θ(n²). Indeed, it is straightforward to use the substitution method to prove that the recurrence T(n) = T(n - 1) Θ(n) has the solution T(n) = Θ(n²).

Thus, if the partitioning is maximally unbalanced at every recursive level of the algorithm, the running time is Θ(n²). Therefore the worst-case running time of quicksort is no better than that of insertion sort. Moreover, the Θ(n²) running time occurs when the input array is already completely sorted-a common situation in which insertion sort runs in O(n) time.

Best-case partitioning

In the most even possible split, PARTITION produces two subproblems, each of size no more than n/2, since one is of size ⌊n/2⌋and one of size ⌈n/2⌉- 1. In this case, quicksort runs much faster. The recurrence for the running time is then

T(n) ≤ 2T (n/2) Θ(n) ,

which by case 2 of the master theorem has the solution T (n) = O(n lg n). Thus, the equal balancing of the two sides of the partition at every level of the recursion produces an asymptotically faster algorithm.

Balanced partitioning

The average-case running time of quicksort is much closer to the best case than to the worst case. The key to understanding why is to understand how the balance of the partitioning is reflected in the recurrence that describes the running time.

Suppose, for example, that the partitioning algorithm always produces a 9-to-1 proportional split, which at first blush seems quite unbalanced. We then obtain the recurrence

T(n) ≤ T (9n/10) T (n/10) cn

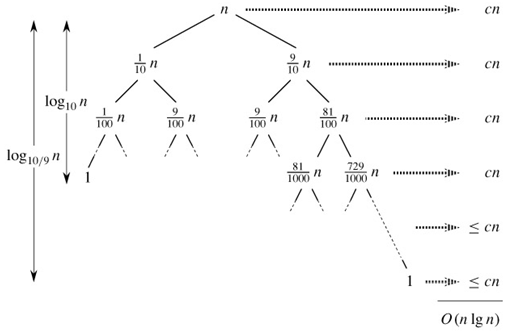
on the running time of quicksort, where we have explicitly included the constant c hidden in the Θ(n) term. Figure 7.4 shows the recursion tree for this recurrence. Notice that every level of the tree has cost cn, until a boundary condition is reached at depth log₁₀n = Θ(lgn), and then the levels have cost at most cn. The recursion terminates at depth log_10/9n = Θ(lg n). The total cost of quicksort is therefore O(n lg n). Thus, with a 9-to-1 proportional split at every level of recursion, which intuitively seems quite unbalanced, quicksort runs in O(n lg n) time-asymptotically the same as if the split were right down the middle. In fact, even a 99-to-1 split yields an O(n lg n) running time. The reason is that any split of constant proportionality yields a recursion tree of depth Θ(lg n), where the cost at each level is O(n). The running time is therefore O(n lg n) whenever the split has constant proportionality.