Probabilistic Analysis And Further Uses Of Indicator Random Variables

Inequality (3.11), 1 x ≤ e_x, gives us

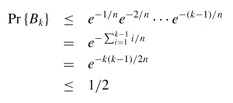
when -k(k - 1)/2n ≤ ln(1/2). The probability that all k birthdays are distinct is at most 1/2 when k(k - 1) = 2n ln 2 or, solving the quadratic equation, when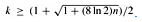 . For n = 365, we must have k ≥ 23. Thus, if at least 23 people are in a room, the probability is at least 1/2 that at least two people have the same birthday. On Mars, a year is 669 Martian days long; it therefore takes 31 Martians to get the same effect.

An analysis using indicator random variables

We can use indicator random variables to provide a simpler but approximate analysis of the birthday paradox. For each pair (i, j) of the k people in the room, we define the indicator random variable X_ij, for 1 ≤ i < j ≤ k, by

By equation (5.7),the probability that two people have matching birthdays is 1/n, and thus by Lemma 5.1, we have

Letting X be the random variable that counts the number of pairs of individuals having the same birthday, we have

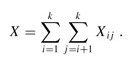
Taking expectations of both sides and applying linearity of expectation, we obtain

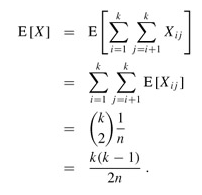
When k(k - 1) ≥ 2n, therefore, the expected number of pairs of people with the same birthday is at least 1. Thus, if we have at least individuals in a room, we can expect at least two to have the same birthday. For n = 365, if k = 28, the expected number of pairs with the same birthday is (28 · 27)/(2 · 365) ≈ 1.0356.

Thus, with at least 28 people, we expect to find at least one matching pair of birth-days. On Mars, where a year is 669 Martian days long, we need at least 38 Martians.

The first analysis, which used only probabilities, determined the number of people required for the probability to exceed 1/2 that a matching pair of birthdays exists, and the second analysis, which used indicator random variables, determined the number such that the expected number of matching birthdays is 1. Although the exact numbers of people differ for the two situations, they are the same asymptotically: 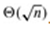.