Properties Of Matrices

Matrices and vectors: A matrix is a rectangular array of numbers. For example,

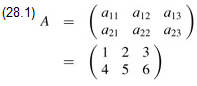
is a 2 × 3 matrix A = (a_ij), where for i = 1, 2 and j = 1, 2, 3, the element of the matrix in row i and column j is a_ij. We use uppercase letters to denote matrices and corresponding subscripted lowercase letters to denote their elements. The set of all m × n matrices with real-valued entries is denoted R^m×n. In general, the set of m × n matrices with entries drawn from a set S is denoted S^m×n.

The transpose of a matrix A is the matrix A^T obtained by exchanging the rows and columns of A. For the matrix A of equation (28.1),

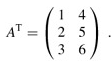
A vector is a one-dimensional array of numbers. For example,

is a vector of size 3. We use lowercase letters to denote vectors, and we denote the ith element of a size-n vector x by x_i , for i = 1, 2, . . . , n. We take the standard form of a vector to be as a column vector equivalent to an n × 1 matrix; the corresponding row vector is obtained by taking the transpose:

x^T = (2 3 5).

The unit vector e_i is the vector whose ith element is 1 and all of whose other elements are 0. Usually, the size of a unit vector is clear from the context.

A zero matrix is a matrix whose every entry is 0. Such a matrix is often denoted 0, since the ambiguity between the number 0 and a matrix of 0's is usually easily resolved from context. If a matrix of 0's is intended, then the size of the matrix also needs to be derived from the context. Square n × n matrices arise frequently. Several special cases of square matrices are of particular interest:

1. A diagonal matrix has a_ij = 0 whenever i ≠ j. Because all of the off-diagonal elements are zero, the matrix can be specified by listing the elements along the diagonal:

2. 

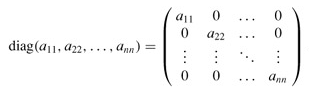
3. The n × n identity matrix I_n is a diagonal matrix with 1's along the diagonal:

4. 

5. When I appears without a subscript, its size can be derived from context. The ith column of an identity matrix is the unit vector e_i.

6. A tridiagonal matrix T is one for which t_ij = 0 if |i - j| > 1. Nonzero entries appear only on the main diagonal, immediately above the main diagonal (t_{i,i 1} for i = 1, 2, . . . , n - 1), or immediately below the main diagonal (t_{i 1,i} for i = 1, 2, . . . , n - 1):

7.