Randomly Built Binary Search Trees
Randomly built binary search trees: We have shown that all the basic operations on a binary search tree run in O(h) time, where h is the height of the tree. The height of a binary search tree varies, however, as items are inserted and deleted. If, for example, the items are inserted in strictly increasing order, the tree will be a chain with height n - 1.
Unfortunately, little is known about the average height of a binary search tree when both insertion and deletion are used to create it. When the tree is created by insertion alone, the analysis becomes more tractable. Let us therefore define a randomly built binary search tree on n keys as one that arises from inserting the keys in random order into an initially empty tree, where each of the n! permutations of the input keys is equally likely. In this section, we shall show that the expected height of a randomly built binary search tree on n keys is O(lg n). We assume that all keys are distinct.
We start by defining three random variables that help measure the height of a randomly built binary search tree. We denote the height of a randomly built binary search on n keys by Xn, and we define the exponential height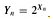 
. When we build a binary search tree on n keys, we choose one key as that of the root, and we let Rn denote the random variable that holds this key's rank within the set of n keys. The value of Rn is equally likely to be any element of the set {1, 2, ..., n}. If Rn = i, then the left subtree of the root is a randomly built binary search tree on i - 1 keys, and the right subtree is a randomly built binary search tree on n - i keys. Because the height of a binary tree is one more than the larger of the heights of the two subtrees of the root, the exponential height of a binary tree is twice the larger of the exponential heights of the two subtrees of the root. If we know that Rn = i, we therefore have that
Yn = 2 · max(Yi-1, Yn-i).
As base cases, we have Y1 = 1, because the exponential height of a tree with 1 node is 20 = 1 and, for convenience, we define Y0 = 0.
Next we define indicator random variables Zn,1, Zn,2, ..., Zn,n, where
Zn,i = I{Rn = i}.
Because Rn is equally likely to be any element of {1, 2, ..., n}, we have that Pr{Rn = i} = 1/n for i = 1,2, ..., n, and hence,
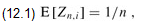
for i = 1, 2, ..., n. Because exactly one value of Zn,i is 1 and all others are 0, we also have
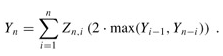
We will show that E[Yn] is polynomial in n, which will ultimately imply that E[Xn] = O(lg n).
The indicator random variable Zn,i = I{Rn = i} is independent of the values of Yi-1 and Yn-i. Having chosen Rn = i, the left subtree, whose exponential height is Yi-1, is randomly built on the i - 1 keys whose ranks are less than i. This subtree is just like any other randomly built binary search tree on i - 1 keys. Other than the number of keys it contains, this subtree's structure is not affected at all by the choice of Rn = i; hence the random variables Yi-1 and Zn,i are independent. Likewise, the right subtree, whose exponential height is Yn-i, is randomly built on the n - i keys whose ranks are greater than i. Its structure is independent of the value of Rn, and so the random variables Yn-i and Zn,i are independent. Hence,
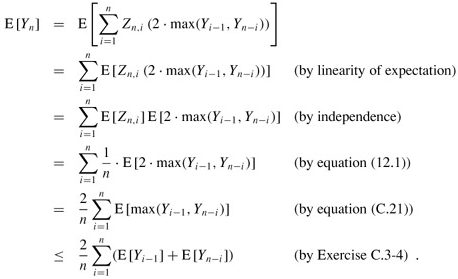
Each term E[Y0], E[Y1], ..., E[Yn-1] appears twice in the last summation, once as E[Yi-1] and once as E[Yn-i], and so we have the recurrence
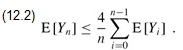
Using the substitution method, we will show that for all positive integers n, the recurrence (12.2) has the solution
