Rotations Of Red Black Tree

Rotations: The search-tree operations TREE-INSERT and TREE-DELETE, when run on a red-black tree with n keys, take O(lg n) time. Because they modify the tree, the result may violate the red-black properties enumerated in Section 13.1. To restore these properties, we must change the colors of some of the nodes in the tree and also change the pointer structure.

We change the pointer structure through rotation, which is a local operation in a search tree that preserves the binary-search-tree property. Figure 13.2 shows the two kinds of rotations: left rotations and right rotations. When we do a left rotation on a node x, we assume that its right child y is not nil[T]; x may be any node in the tree whose right child is not nil[T]. The left rotation "pivots" around the link from x to y. It makes y the new root of the subtree, with x as y's left child and y's left child as x's right child.

Figure 13.2: The rotation operations on a binary search tree. The operation LEFT-ROTATE(T, x) transforms the configuration of the two nodes on the left into the configuration on the right by changing a constant number of pointers. The configuration on the right can be transformed into the configuration on the left by the inverse operation RIGHT-ROTATE(T, y). The letters α, β, and γ represent arbitrary subtrees. A rotation operation preserves the binary-search-tree property: the keys in α precede key[x], which precedes the keys in β, which precede key[y], which precedes the keys in γ.

The pseudocode for LEFT-ROTATE assumes that right[x] ≠ nil[T] and that the root's parent is nil[T].

	LEFT-ROTATE(T, x)
 1  y ← right[x]            ▹ Set y.
 2  right[x] ← left[y]      ▹ Turn y's left subtree into x's right subtree.
 3  p[left[y]] ← x
 4  p[y] ← p[x]             ▹ Link x's parent to y.
 5  if p[x] = nil[T]
 6     then root[T] ← y
 7     else if x = left[p[x]]
 8             then left[p[x]] ← y
 9             else right[p[x]] ← y
10  left[y] ← x             ▹ Put x on y's left.
11  p[x] ← y

Figure 13.3 shows how LEFT-ROTATE operates. The code for RIGHT-ROTATE is symmetric. Both LEFT-ROTATE and RIGHT-ROTATE run in O(1) time. Only pointers are changed by a rotation; all other fields in a node remain the same.

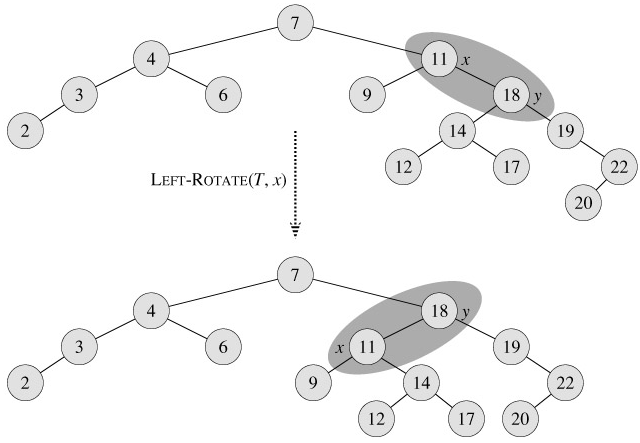
Figure 13.3: An example of how the procedure LEFT-ROTATE(T, x) modifies a binary search tree. Inorder tree walks of the input tree and the modified tree produce the same listing of key values.