Selection In Worst-case Linear Time

Selection in worst-case linear time: We now examine a selection algorithm whose running time is O(n) in the worst case. Like RANDOMIZED-SELECT, the algorithm SELECT finds the desired element by recursively partitioning the input array. The idea behind the algorithm, however, is to guarantee a good split when the array is partitioned. SELECT uses the deterministic partitioning algorithm PARTITION from quicksort, modified to take the element to partition around as an input parameter.

The SELECT algorithm determines the ith smallest of an input array of n > 1 elements by executing the following steps. (If n = 1, then SELECT merely returns its only input value as the ith smallest.)

Divide the n elements of the input array into ⌊n/5⌋ groups of 5 elements each and at most one group made up of the remaining n mod 5 elements.
Find the median of each of the ⌈n/5⌉ groups by first insertion sorting the elements of each group (of which there are at most 5) and then picking the median from the sorted list of group elements.
Use SELECT recursively to find the median x of the ⌈n/5⌉ medians found in step 2. (If there are an even number of medians, then by our convention, x is the lower median.)
Partition the input array around the median-of-medians x using the modified version of PARTITION. Let k be one more than the number of elements on the low side of the partition, so that x is the kth smallest element and there are n-k elements on the high side of the partition.
If i = k, then return x. Otherwise, use SELECT recursively to find the ith smallest element on the low side if i < k, or the (i - k)th smallest element on the high side if i > k.

To analyze the running time of SELECT, we first determine a lower bound on the number of elements that are greater than the partitioning element x. Figure 9.1 is helpful in visualizing this bookkeeping. At least half of the medians found in step 2 are greater than the median-of-medians x. Thus, at least half of the ⌈n/5⌉ groups contribute 3 elements that are greater than x, except for the one group that has fewer than 5 elements if 5 does not divide n exactly, and the one group containing x itself. Discounting these two groups, it follows that the number of elements greater than x is at least

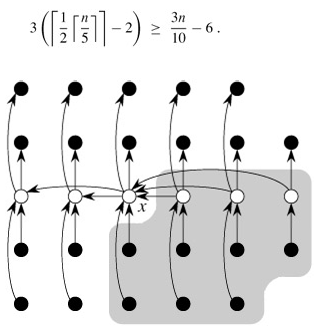
Figure 9.1: Analysis of the algorithm SELECT. The n elements are represented by small circles, and each group occupies a column. The medians of the groups are whitened, and the median-of-medians x is labeled. (When finding the median of an even number of elements, we use the lower median.) Arrows are drawn from larger elements to smaller, from which it can be seen that 3 out of every full group of 5 elements to the right of x are greater than x, and 3 out of every group of 5 elements to the left of x are less than x. The elements greater than x are shown on a shaded background.

Similarly, the number of elements that are less than x is at least 3n/10 - 6. Thus, in the worst case, SELECT is called recursively on at most 7n/10 6 elements in step 5.

We can now develop a recurrence for the worst-case running time T(n) of the algorithm SELECT. Steps 1, 2, and 4 take O(n) time. (Step 2 consists of O(n) calls of insertion sort on sets of size O(1).) Step 3 takes time T(⌈n/5⌉), and step 5 takes time at most T(7n/10 6), assuming that T is monotonically increasing. We make the assumption, which seems unmotivated at first, that any input of 140 or fewer elements requires O(1) time; the origin of the magic constant 140 will be clear shortly. We can therefore obtain the recurrence

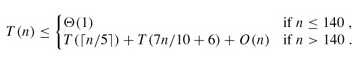
We show that the running time is linear by substitution. More specifically, we will show that T(n) ≤ cn for some suitably large constant c and all n > 0. We begin by assuming that T(n) ≤ cn for some suitably large constant c and all n ≤ 140; this assumption holds if c is large enough. We also pick a constant a such that the function described by the O(n) term above (which describes the non-recursive component of the running time of the algorithm) is bounded above by an for all n > 0. Substituting this inductive hypothesis into the right-hand side of the recurrence yields

T(n)	≤	c ⌈n/5⌉ c(7n/10 6) an
	≤	cn/5 c 7cn/10 6c an
	=	9cn/10 7c an
	=	cn (-cn/10 7c an) ,

which is at most cn if

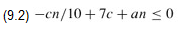
Inequality (9.2) is equivalent to the inequality c ≥ 10a(n/(n - 70)) when n > 70. Because we assume that n ≥ 140, we have n/(n - 70) ≤ 2, and so choosing c ≥ 20a will satisfy inequality (9.2). (Note that there is nothing special about the constant 140; we could replace it by any integer strictly greater than 70 and then choose c accordingly.) The worst-case running time of SELECT is therefore linear.