Single-source Shortest Paths In Directed Acyclic Graphs

Single-source shortest paths in directed acyclic graphs

By relaxing the edges of a weighted dag (directed acyclic graph) G = (V, E) according to a topological sort of its vertices, we can compute shortest paths from a single source in Θ(V E) time. Shortest paths are always well defined in a dag, since even if there are negative-weight edges, no negative-weight cycles can exist.

The algorithm starts by topologically sorting the dag to impose a linear ordering on the vertices. If there is a path from vertex u to vertex v, then u precedes v in the topological sort. We make just one pass over the vertices in the topologically sorted order. As we process each vertex, we relax each edge that leaves the vertex.

DAG-SHORTEST-PATHS(G, w, s)
1  topologically sort the vertices of G
2  INITIALIZE-SINGLE-SOURCE(G, s)
3  for each vertex u, taken in topologically sorted order
4       do for each vertex v ∈ Adj[u]
5              do RELAX(u, v, w)

Figure 24.5 shows the execution of this algorithm.

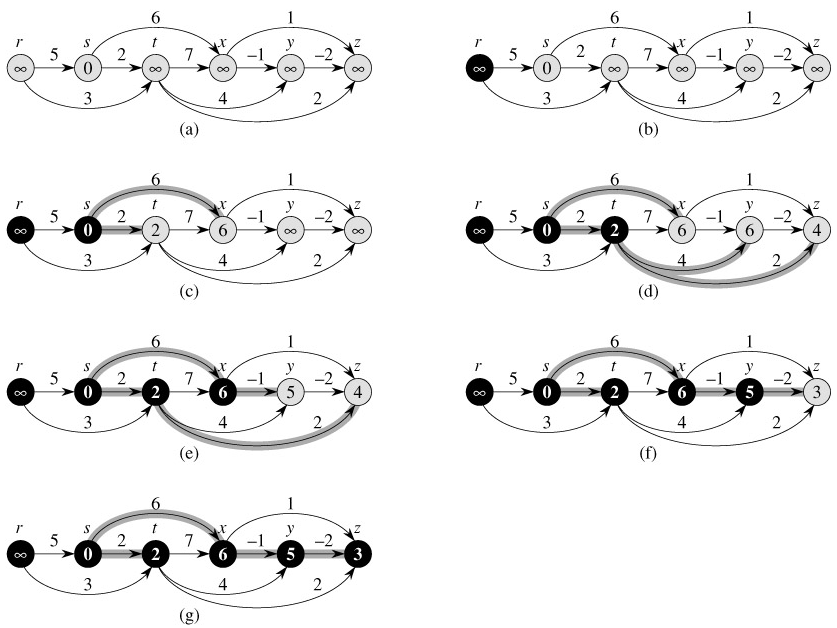
Figure 24.5: The execution of the algorithm for shortest paths in a directed acyclic graph. The vertices are topologically sorted from left to right. The source vertex is s. The d values are shown within the vertices, and shaded edges indicate the π values. (a) The situation before the first iteration of the for loop of lines 3-5. (b)-(g) The situation after each iteration of the for loop of lines 3-5. The newly blackened vertex in each iteration was used as u in that iteration. The values shown in part (g) are the final values.

The running time of this algorithm is easy to analyze. As shown in Section 22.4, the topological sort of line 1 can be performed in Θ(V E) time. The call of INITIALIZE-SINGLE-SOURCE in line 2 takes Θ(V) time. There is one iteration per vertex in the for loop of lines 3-5. For each vertex, the edges that leave the vertex are each examined exactly once. Thus, there are a total of |E| iterations of the inner for loop of lines 4-5. (We have used an aggregate analysis here.) Because each iteration of the inner for loop takes Θ(1) time, the total running time is Θ(V E), which is linear in the size of an adjacency-list representation of the graph.

The following theorem shows that the DAG-SHORTEST-PATHS procedure correctly computes the shortest paths.